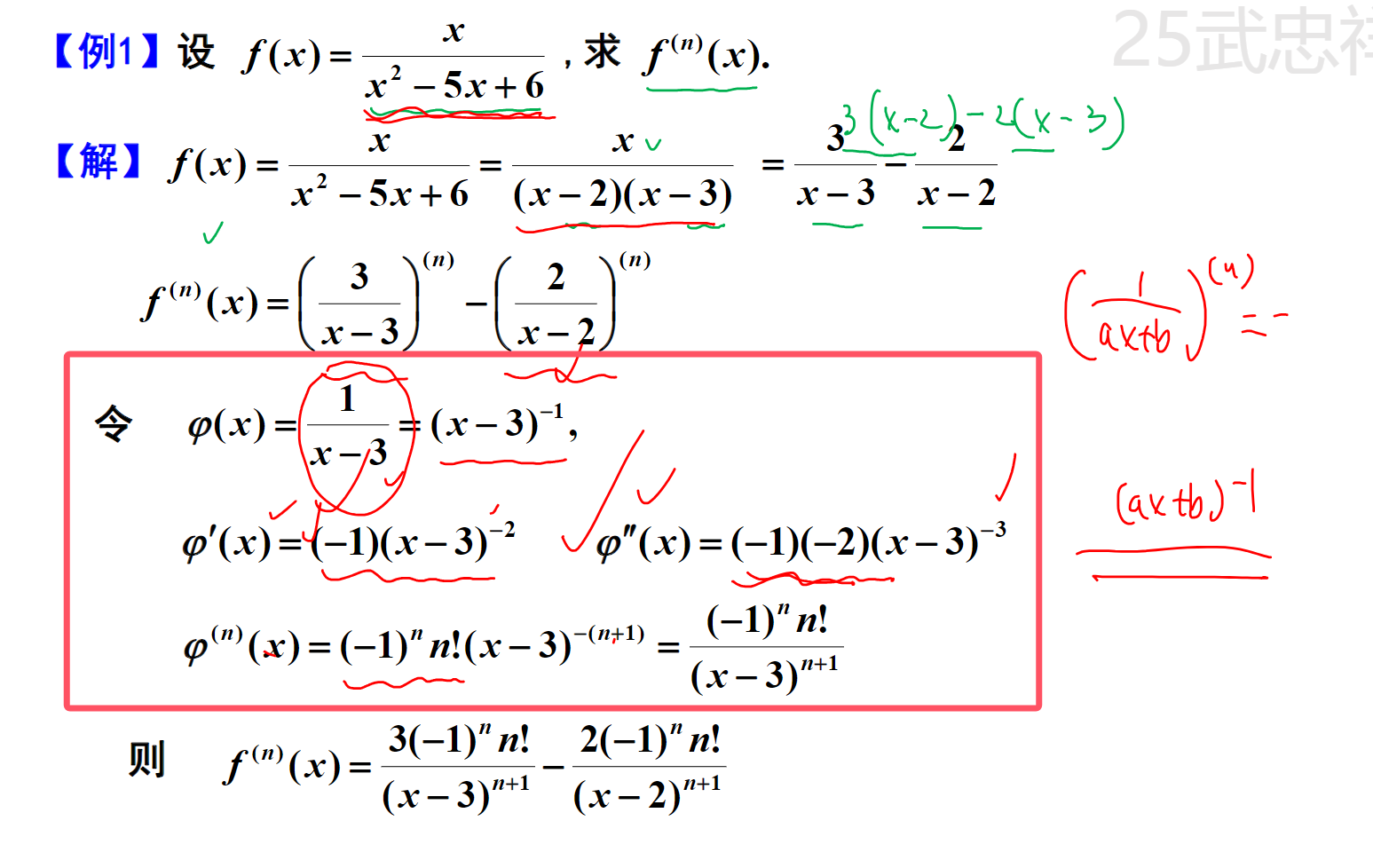高阶导数问题
泰勒展开式
f(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+3!f′′′(a)(x−a)3+⋯+n!f(n)(a)(x−a)n+⋯
ex=n=0∑∞n!xn=1+x+2!x2+3!x3+⋯+n!xn+⋯(−∞<x<+∞)
ln(1+x)=n=1∑∞(−1)n−1nxn=x−2x2+3x3−4x4+⋯+(−1)n−1nxn+⋯(−1<x≤1)
1+x1=n=0∑∞(−1)nxn=1−x+x2−x3+⋯+(−1)nxn+⋯(−1<x<1)
1−x1=n=0∑∞xn=1+x+x2+x3+⋯+xn+⋯(−1<x<1)
(1+x)α=1+αx+2!α(α−1)x2+3!α(α−1)(α−2)x3+⋯+n!α(α−1)⋯(α−n+1)xn+⋯,⎩⎨⎧x∈(−1,1),x∈(−1,1],x∈[−1,1],x∈R,α≤−1−1<α<0α>0,α∈/N+α∈N+
sin(x)=n=0∑∞(−1)n(2n+1)!x2n+1=x−3!x3+5!x5−7!x7+⋯+(−1)n(2n+1)!x2n+1+⋯(−∞<x<+∞)
cos(x)=n=0∑∞(−1)n(2n)!x2n=1−2!x2+4!x4−6!x6+⋯+(−1)n(2n)!x2n+⋯(−∞<x<+∞)
tan(x)=x+31x3+⋯
arcsin(x)=x+61x3+⋯
arctan(x)=x−31x3+⋯
莱布尼兹公式
- (uv)(n)=u(n)v+Cn1u(n−1)v′+⋯+Cnku(n−k)v(k)+⋯+uv(n)
莱布尼兹公式不方便时的优雅解法(找规律):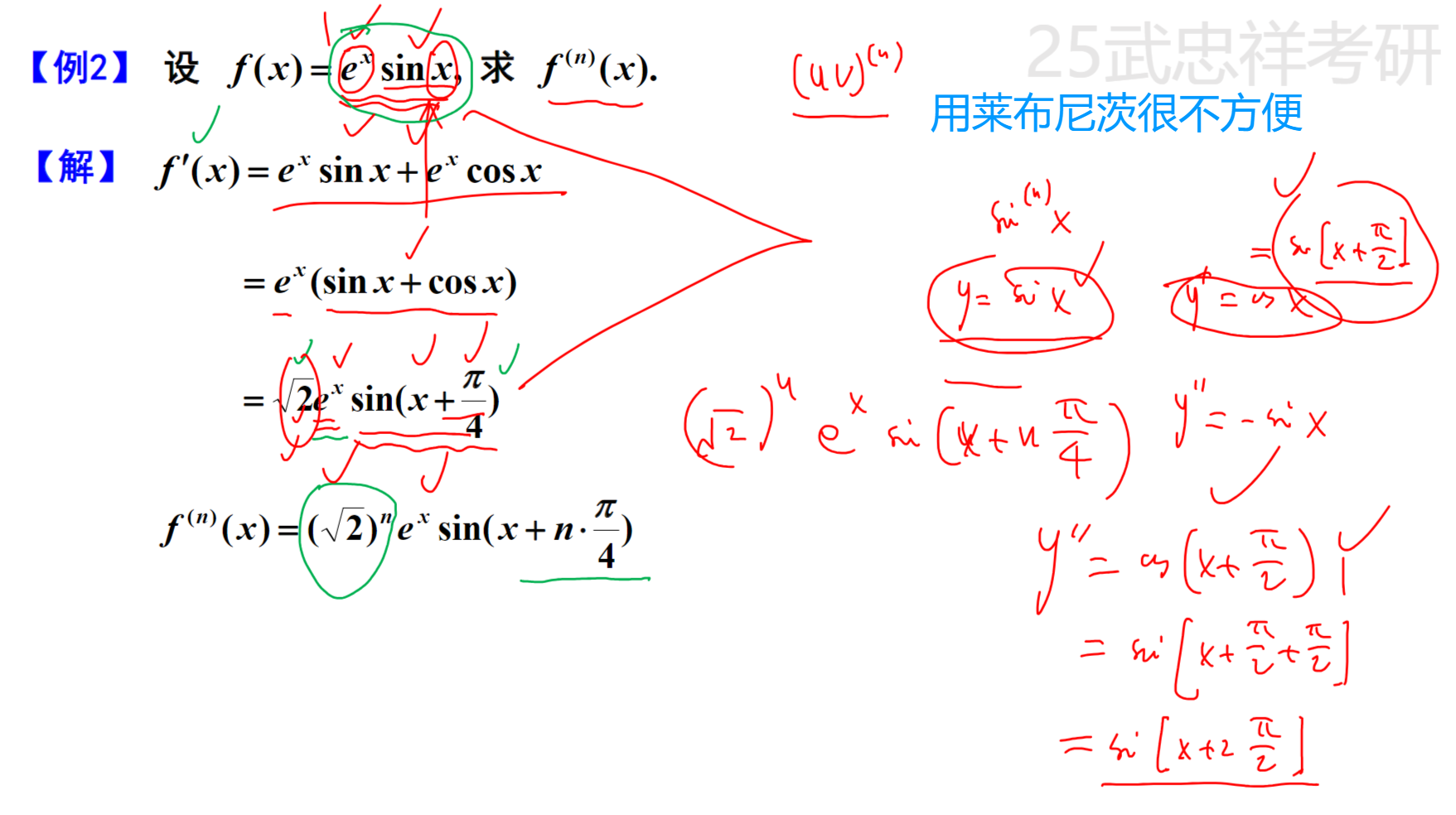
高阶导数在 x≠0 时的值:运用常见初等函数的 n 阶导数公式
求高阶导数在 x≠0 时的值,运用常见初等函数的 n 阶导数公式。这些公式不需要记忆,很容易通过求一次或二次导数,来归纳得到。
- (eax+b)(n)=aneax+b
- (sin(ax+b))(n)=ansin(2nπ+ax+b)
- (cos(ax+b))(n)=ancos(2nπ+ax+b)
- (ln(1+x))(n)=(1+x)n(−1)n−1(n−1)!
- (ln(ax+b))(n)=(−1)n−1an(ax+b)n(n−1)!
- ((1+x)α)(n)=α(α−1)⋯(α−n+1)(1+x)α−n
- (ax+b1)(n)=(−1)nan(ax+b)n+1n!
不用背,直接靠这样推导: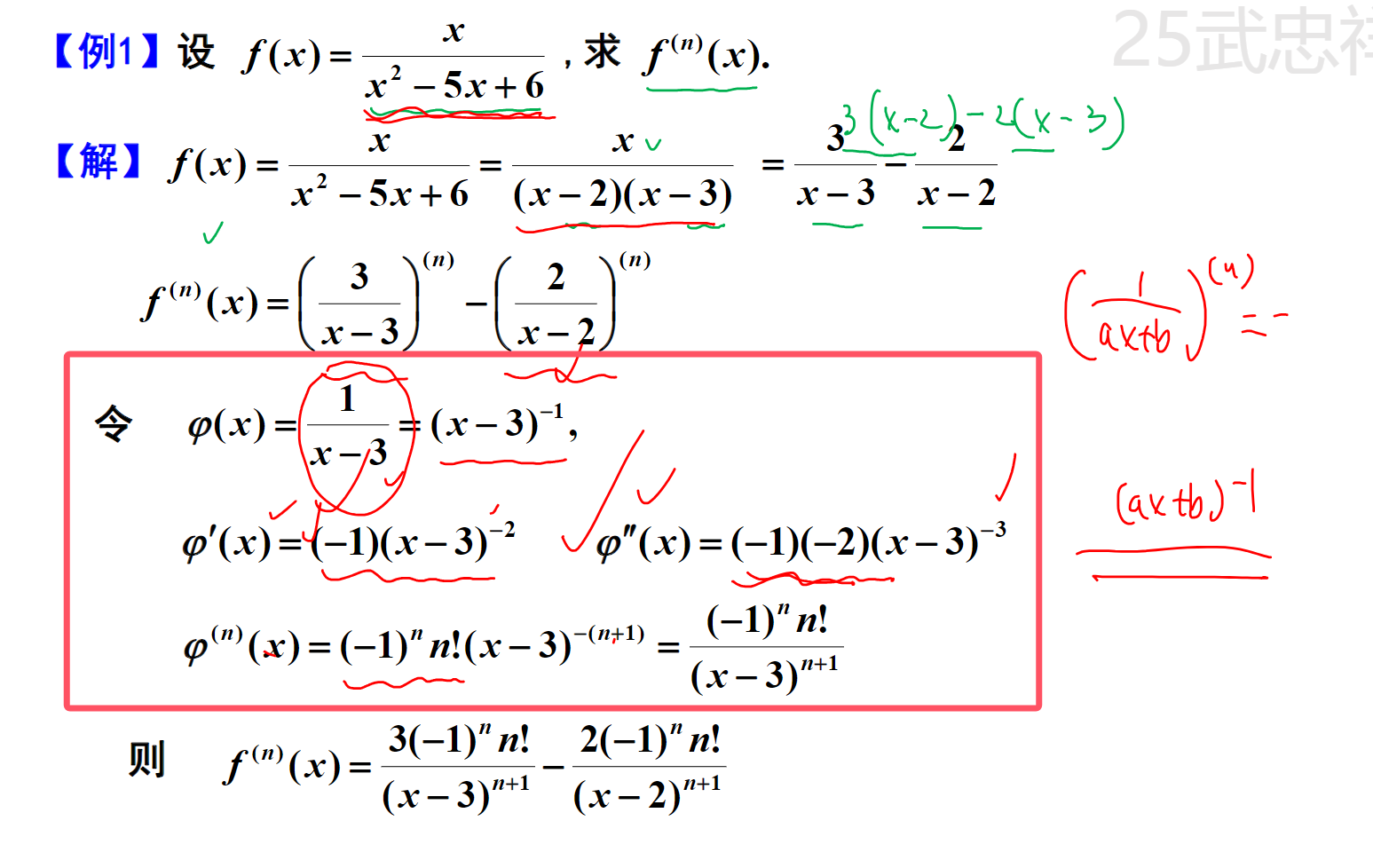
多项式高阶导数在零点的值
- 令 f(x)=(x−x0)n,则 f(n)(x0)=n!,f(k)(x0)=0, (k ≠ n
这里k可以大于n也可以小于n)
积分公式
常用
- ∫x1=2x+C
- ∫axdx=lnaax+C, a>0 且 a ≠ 1
- ∫tanxdx=−ln∣cosx∣+C
- ∫cotxdx=ln∣sinx∣+C
- ∫cosxdx=∫secxdx=ln∣secx+tanx∣+C
- ∫sinxdx=∫cscxdx=ln∣cscx−cotx∣+C
- ∫sec2xdx=tanx+C
- ∫csc2xdx=−cotx+C
- ∫secxtanxdx=secx+C
- ∫cscxcotxdx=−cscx+C
- ∫a2+x21dx=a1arctanax+C
- ∫a2−x21dx=arcsinax+C(a>0)
- ∫x2+a21dx=ln(x+x2+a2)+C (常见a=1)
- ∫x2−a21dx=ln∣x+x2−a2∣+C (|x|>|a|)
- ∫x2−a21dx=2a1ln∣x+ax−a∣+C
- ∫a2−x21dx=2a1ln∣x−ax+a∣+C
- ∫tan2xdx=tanx−x+C(tan2x=sec2x−1) ✏️
- ∫cot2xdx=−cotx−x+C(cot2x=csc2x−1) ✏️
少见
- ∫a2−x2dx=2a2arcsinax+2xa2−x2+C(a>∣x∣≥0)
- ∫sin2xdx=2x−4sin2x+C(sin2x=21−cos2x)
- ∫cos2xdx=2x+4sin2x+C(cos2x=21+cos2x)
特殊的分部积分公式
e^x和sinx&cosx
- ∫eaxsinbxdx=a2+b2(eax)′eax(sinbx)′sinbx+C=a2+b2aeaxsinbx−beaxcosbx+C
- ∫eaxcosbxdx=a2+b2(eax)′eax(cosbx)′cosbx+C=a2+b2aeaxcosbx+beaxsinbx+C
结论
周期
- 设f(x)是以T为周期的连续函数,则对任意的实数a,都有∫aa+Tf(x)dx=∫0Tf(x)dx,即在长度为一个周期的区间上的定积分,与该区间的起点位置无关。
区间再现公式
- 设f(x)为连续函数,则∫abf(x)dx=∫abf(a+b−x)dx
- 证明:令t=a+b-x
还有一个结论可以直接用(根据区间再现公式推出的):∫0πxf(sinx)dx=2π∫0πf(sinx)dx
点火公式 及其 变形
- 末尾为21(n为正偶数),则点火(再乘2π)
- 末尾为1(n为正奇数),则点火失败(不乘,结束)
- ∫0πsinnxdx=2∫02πsinnxdx
证明:∫0πsinnxdx=∫−2π2πsinn(t+2π)d(t+2π)=∫−2π2πcosntdt(cosx为偶函数)=2∫02πcosnxdx=2∫02πsinnxdx
- (n为正偶数)∫0πcosnxdx=2∫02πcosnxdx
证明:∫0πcosnxdx=∫−2π2πcosn(t+2π)d(t+2π)=∫−2π2πsinntdt(sinnx为偶函数)=2∫02πsinnxdx=2∫02πcosnxdx
- (n为正奇数)∫0πcosnxdx=0
证明:同理证到∫−2π2πsinntdt时,因n为奇数,所以sinnx为奇函数
- (n为正奇数)∫02πsinnxdx=∫02πcosnxdx=0
- (n为正偶数)∫02πsinnxdx=∫02πcosnxdx=4∫02πsinnxdx=4∫02πcosnxdx
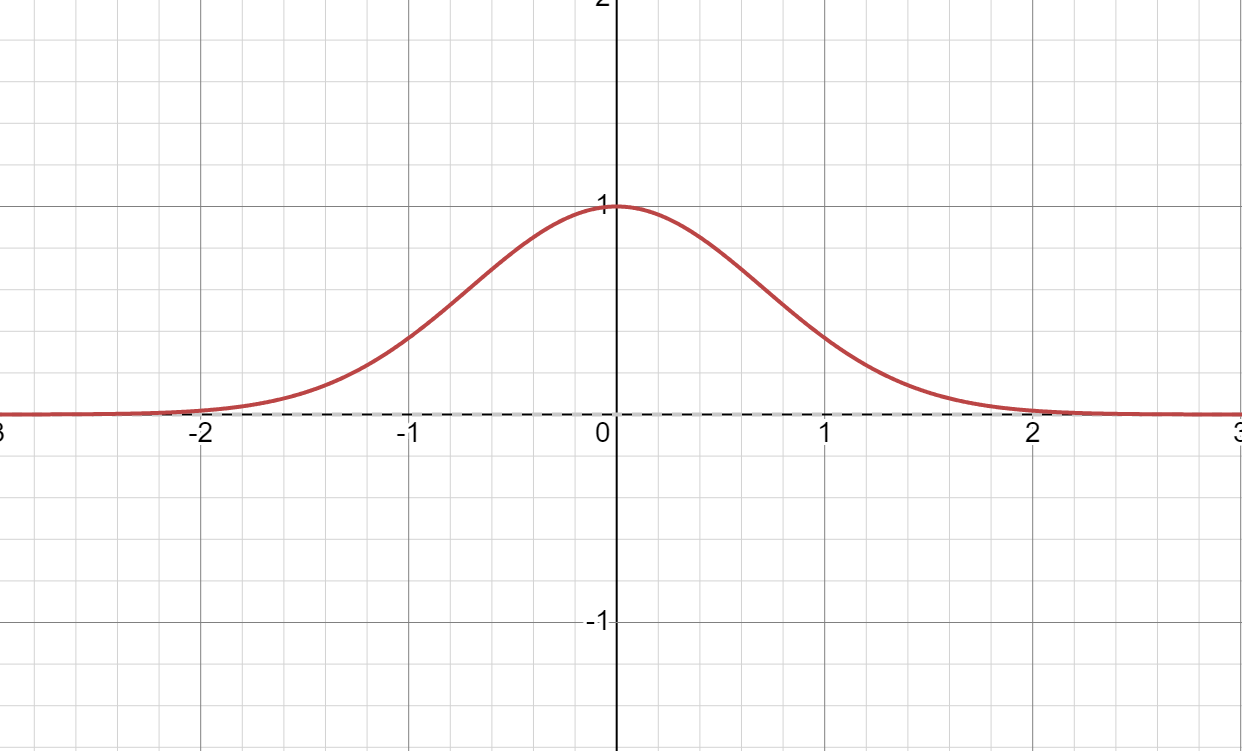
高斯积分
- ∫−∞+∞e−x2dx=π
- ∫−∞0e−x2dx=∫0+∞e−x2dx=2π
- y=e−x2图像如图所示(水平渐近线y=0)
n^(1/n)
- n→∞limnn1=1
奥特曼公式
- 条件:ai(i=1,2,⋯,m)都是非负数
- n→∞limna1n+a2n+⋯+amn=max{a1,a2,⋯,am}.
曲率公式
- 曲率 K=(1+y′2)3/2∣y′′∣
- 曲率半径 r=K1
- 参数方程(x(t),y(t)),曲率 K=[x′2(t)+y′2(t)]3/2∣x′(t)y′′(t)−x′′(t)y′(t)∣
法线斜率
- −y′(x0)1
圆锥曲线
椭圆
a2x2+b2y2=1
其中 a 和 b 分别为椭圆的半长轴和半短轴。
双曲线
a2x2−b2y2=1 或 b2y2−a2x2=1
抛物线
从原点 (0, 0) 平移到任意点 (h, k) 。
以 x 为轴的抛物线的标准方程为:(y−k)2=4p(x−h)
以 y 为轴的抛物线的标准方程为:(x−h)2=4p(y−k)
三角函数图像
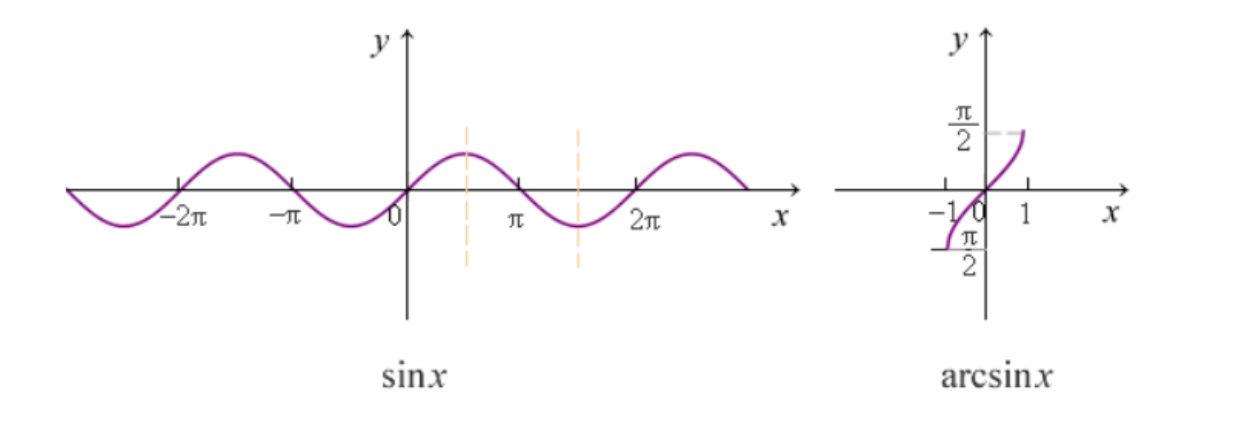
sinx & arcsinx
- 定义域与值域互换,关于y=x对称
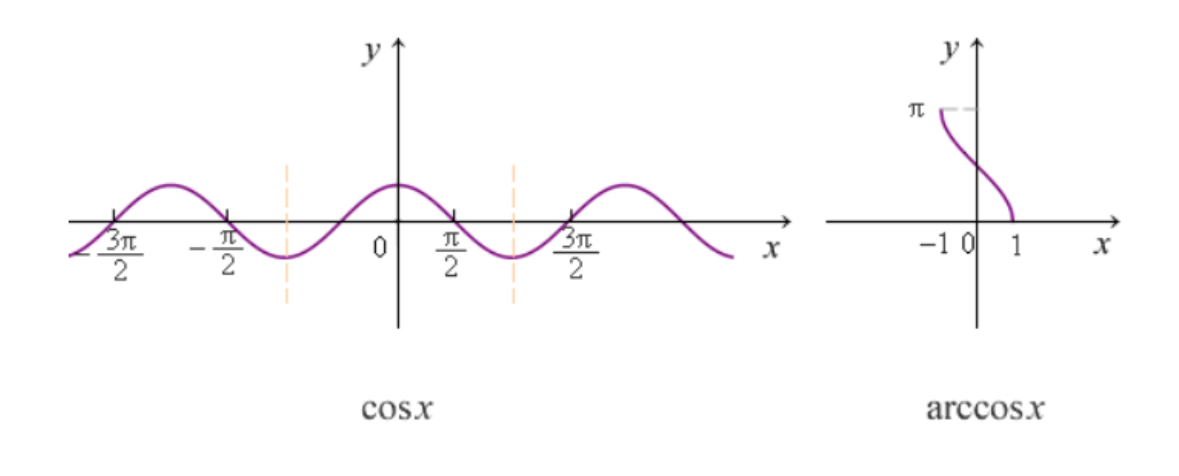
cosx & arccosx
- arccosx没有负的值域,所以比如遇到x=0,大胆写2π ,因为不可能是 −2π。
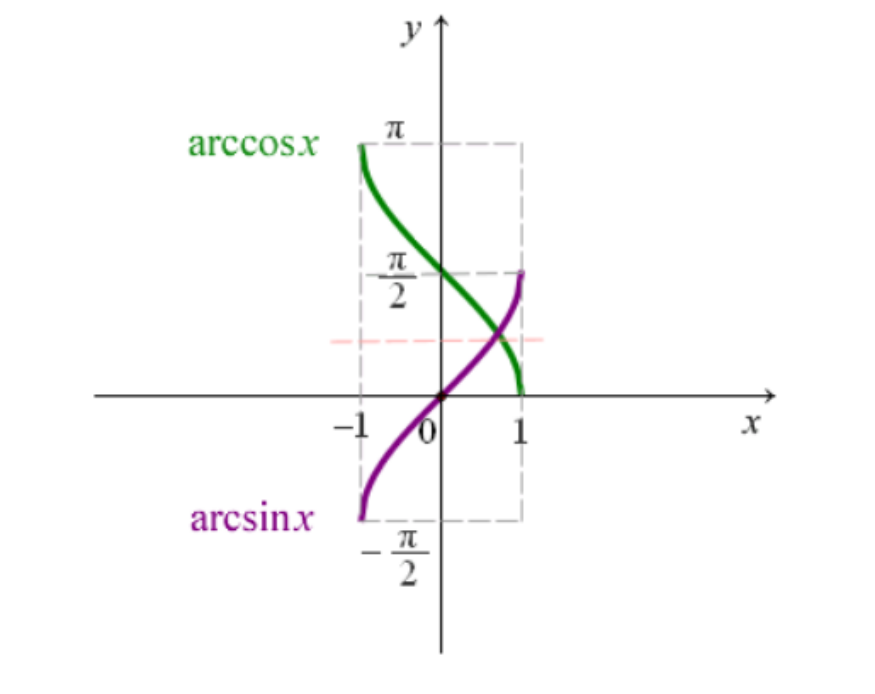
arcsinx & arccosx
- 关于y=4π 对称,相交于点(22,4π)。
- arcsinx+arccosx=2π(−1≤x≤1)
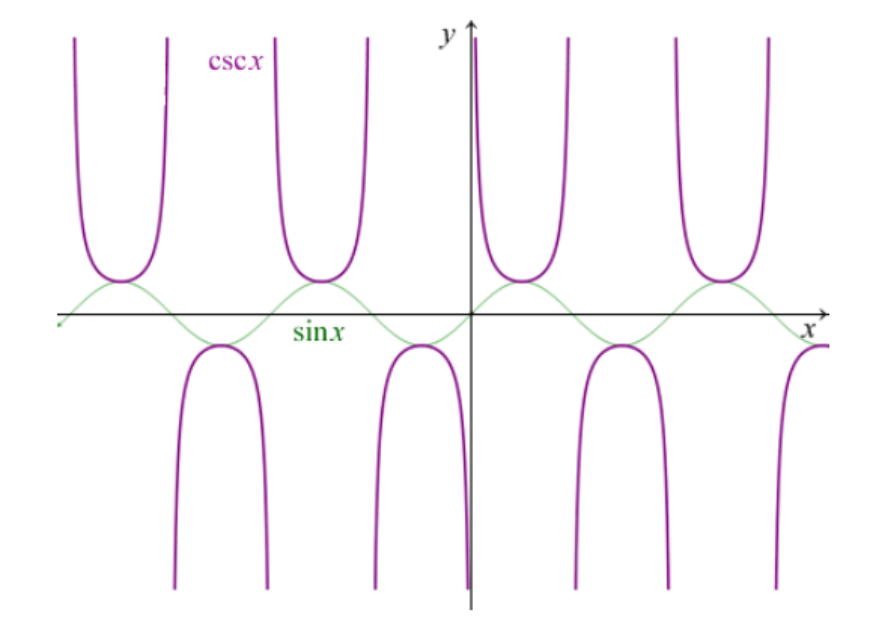
cscx = 1/sinx
- x→kπ时,函数的极限是∞。
secx = 1/cosx
- x→2kπ时,函数的极限是∞。
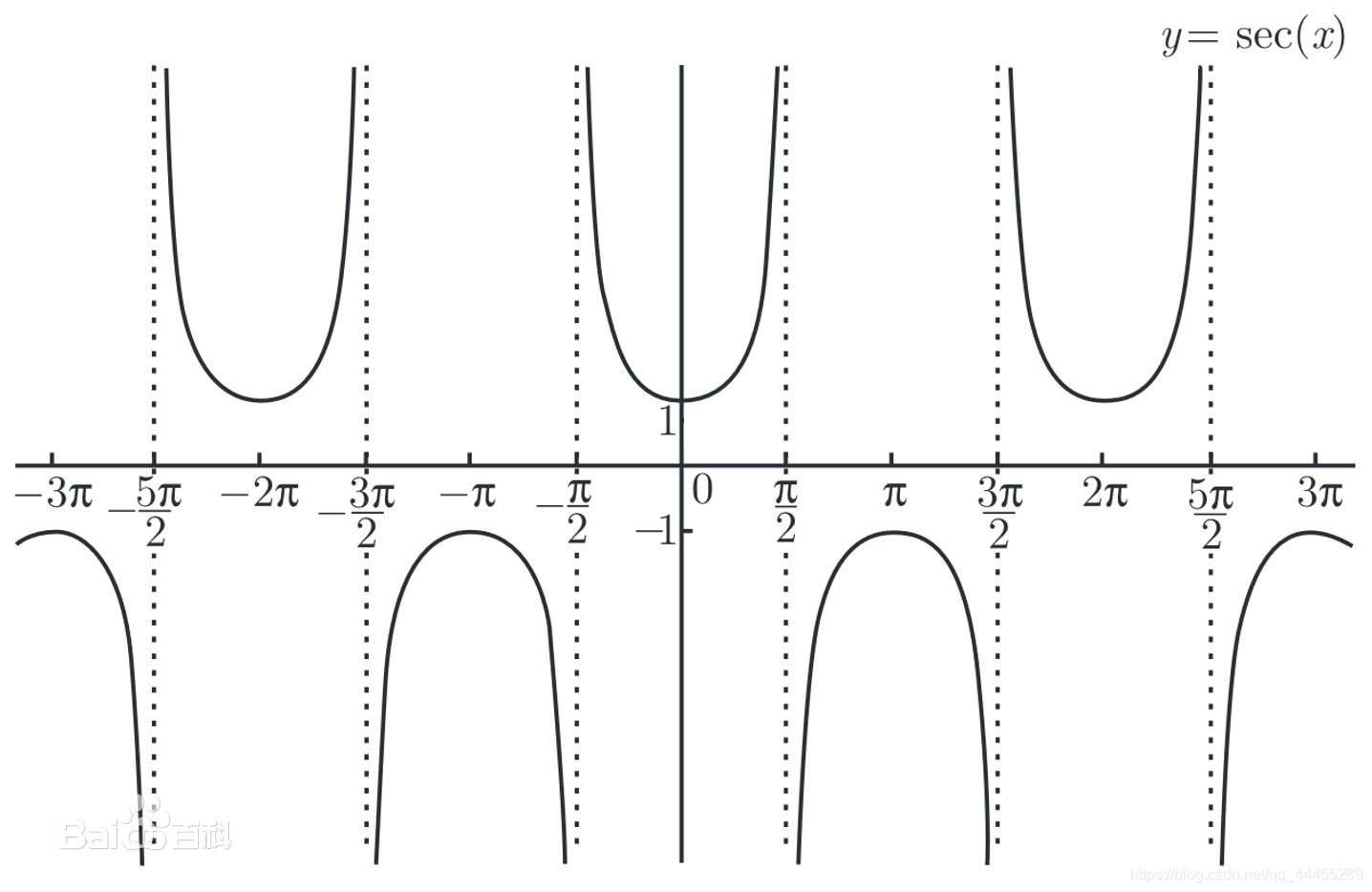
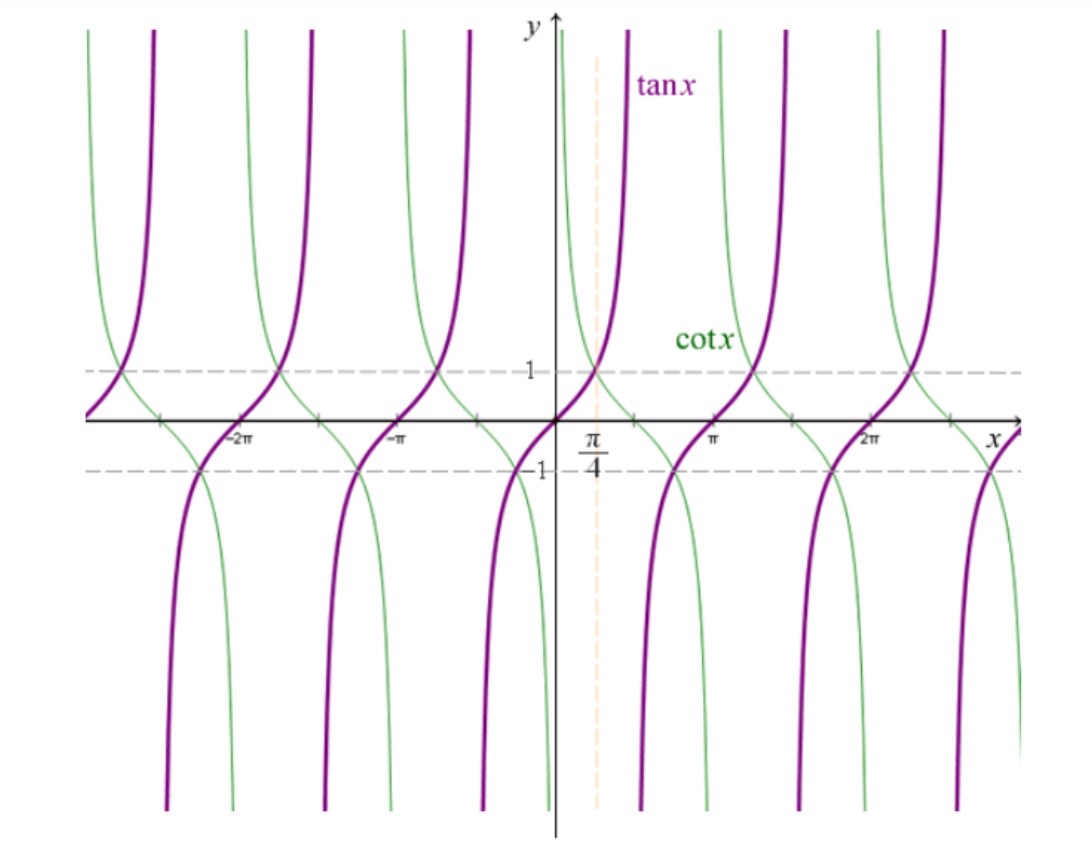
tanx & cotx
- 遇到间断点的题目时,注意tanx和cotx的定义域是不一样的,cotx不能直接根据1/tanx来判断定义域!
- 当x=4π+2kπ 时,y=tanx 和 y=cotx 函数值相等,等于±1。
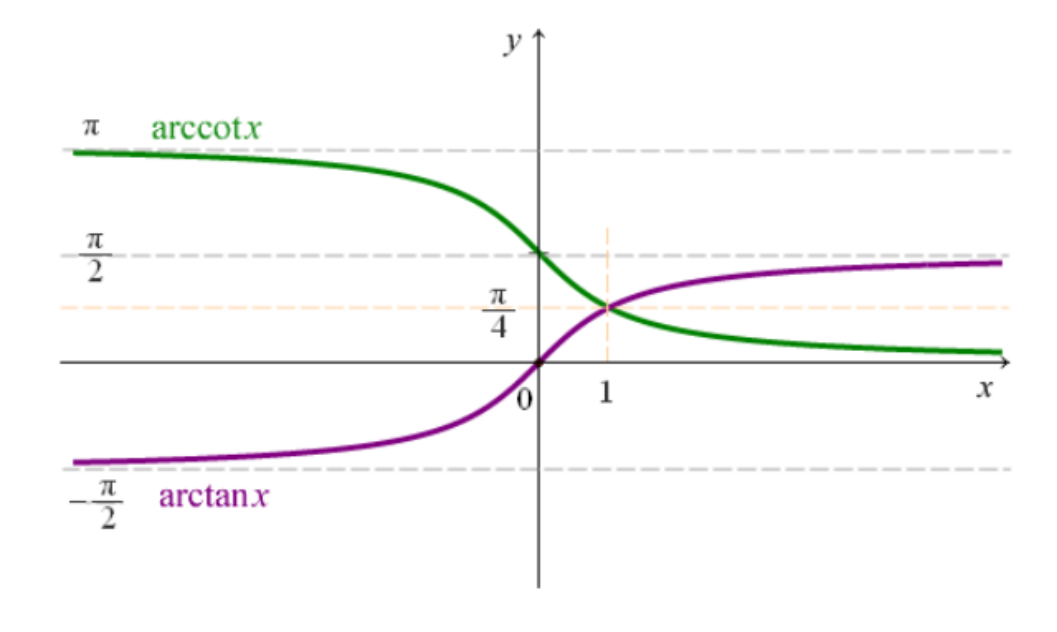
arctanx & arccotx
- −2π<arctanx<2π,0<arccotx<π
- 关于直线 y=4π 对称,相交于点 (1,4π) 。
- arctanx+arccotx=2π(−∞<x<+∞)
韦达定理(已知特征根,求原微分方程)
- 用韦达定理,可以求出原常系数齐次方程的各阶系数。初中所学的韦达定理为二阶,对此熟练掌握,起码能轻松求出二阶方程的各阶系数(只要令a=1即可,因为标准方程最高阶y’’的系数本就该为1)。
- 初中所学的韦达定理:ax2+bx+c=0x1+x2=−ab,x1x2=ac(令a=1)
- 二阶以上的不建议用韦达定理求,主要有i在,相乘的时候也挺麻烦的,老老实实用(λ−λ1)(λ−λ2)⋯(λ−λn)
即可。
和差化积
- sinx+siny=2sin(2x+y)cos(2x−y)
- sinx−siny=2cos(2x+y)sin(2x−y)
- cosx+cosy=2cos(2x+y)cos(2x−y)
- cosx−cosy=−2sin(2x+y)sin(2x−y)
注意事项
- 看到lnx,想到x>0
- ∣u∣=u2
- ln(u1u2u3)=lnu1+lnu2+lnu3
取整函数
- y=[x] 为取整函数(向下取整),取不超过x的最大整数。
- [−1.99]=−2
- [x+n]=[x]+n,其中n为整数
- x−1<[x]≤x
- x→0+lim[x]=0;x→0−lim[x]=−1
常用的放缩不等式
转自知乎-常用的放缩不等式
指数函数放缩
放缩成一次函数
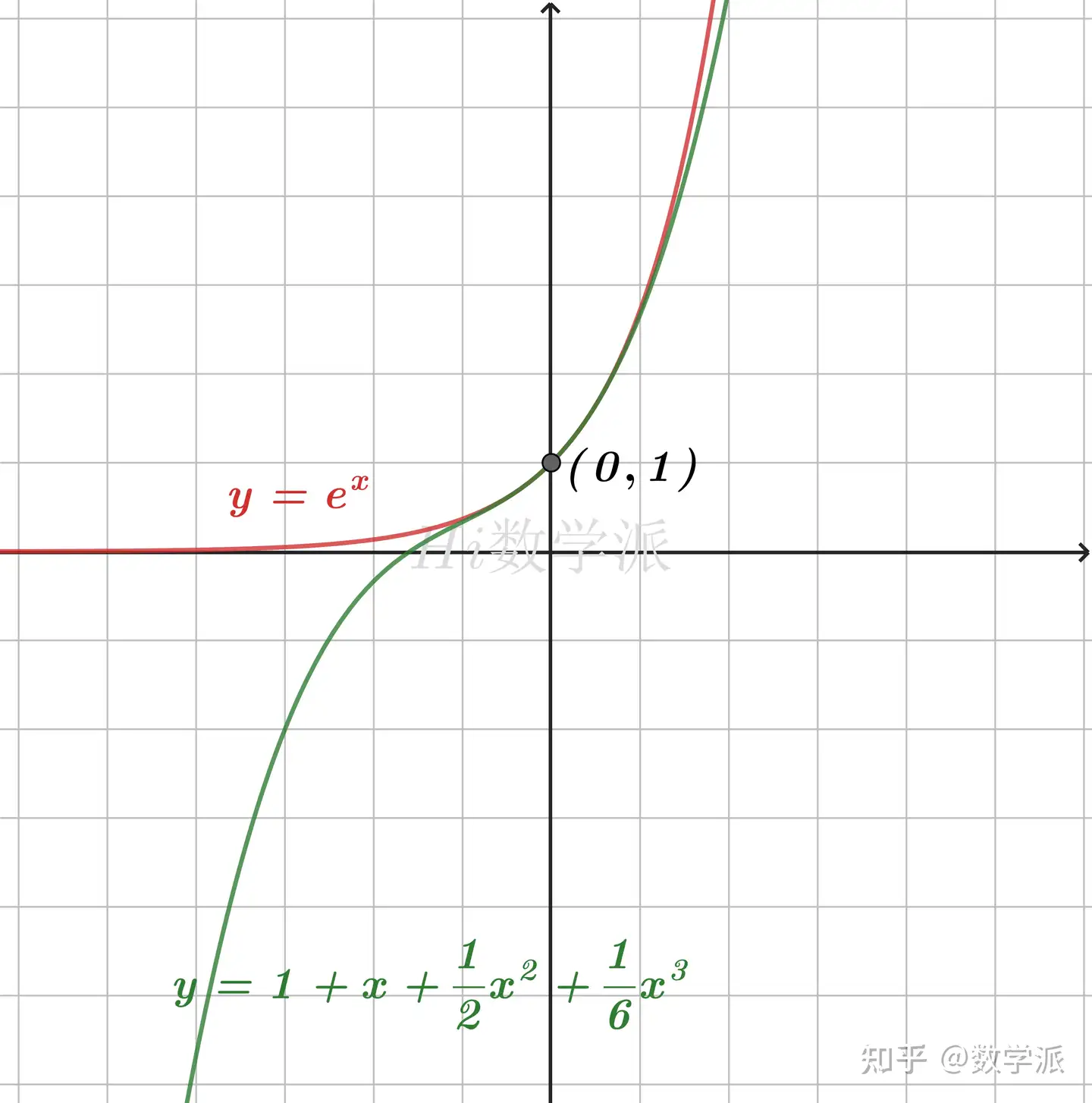
- ex≥x+1>x (仅当x=0时取等号)
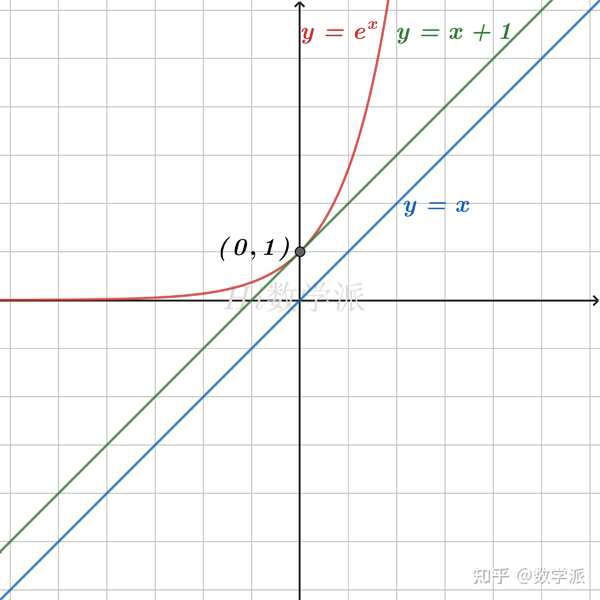
- ex≥ex (仅当x=1时取等号)
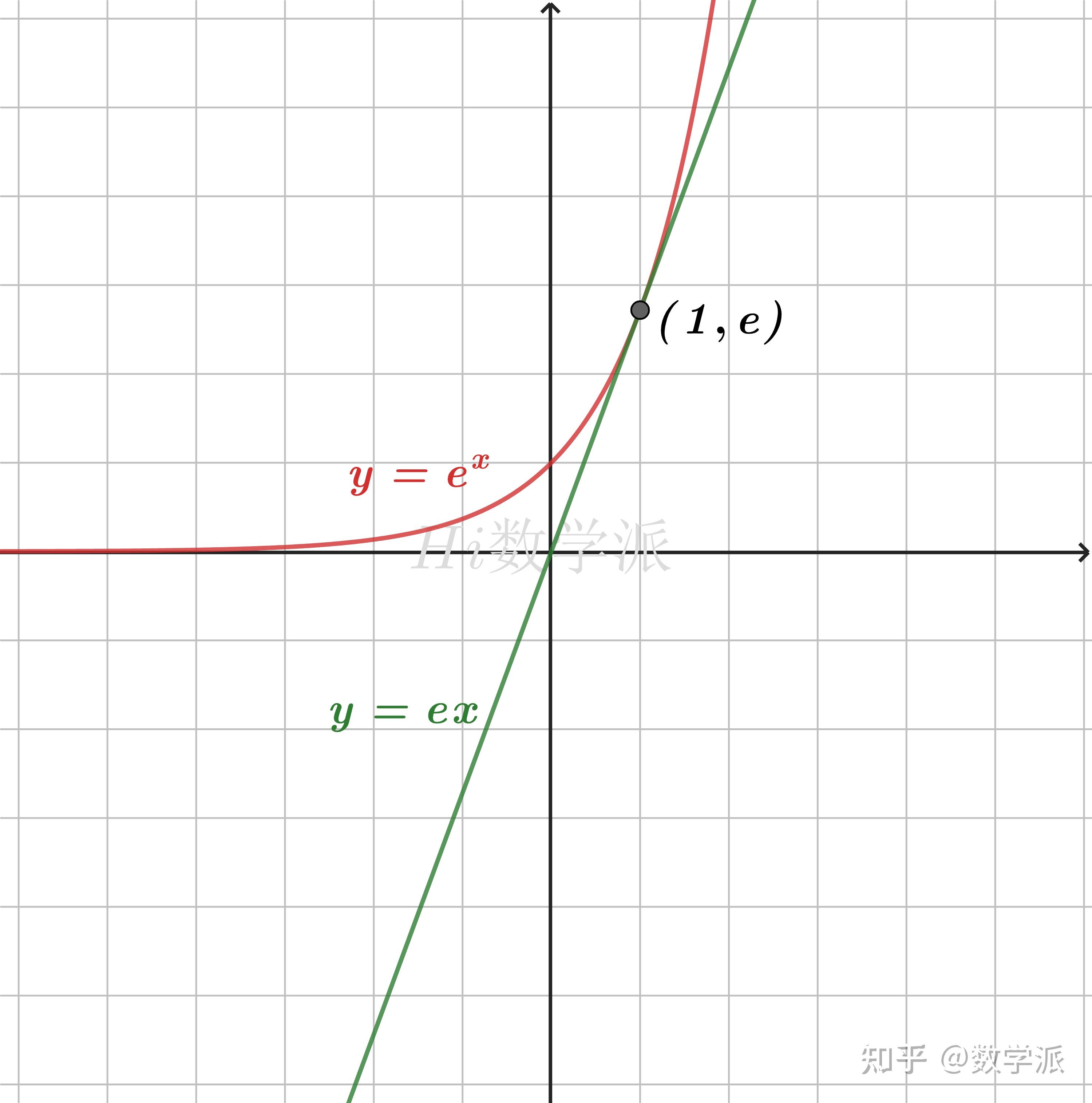
放缩成反比例函数
- ex≤1−x1,(x<1) (仅当x=0时取等号)
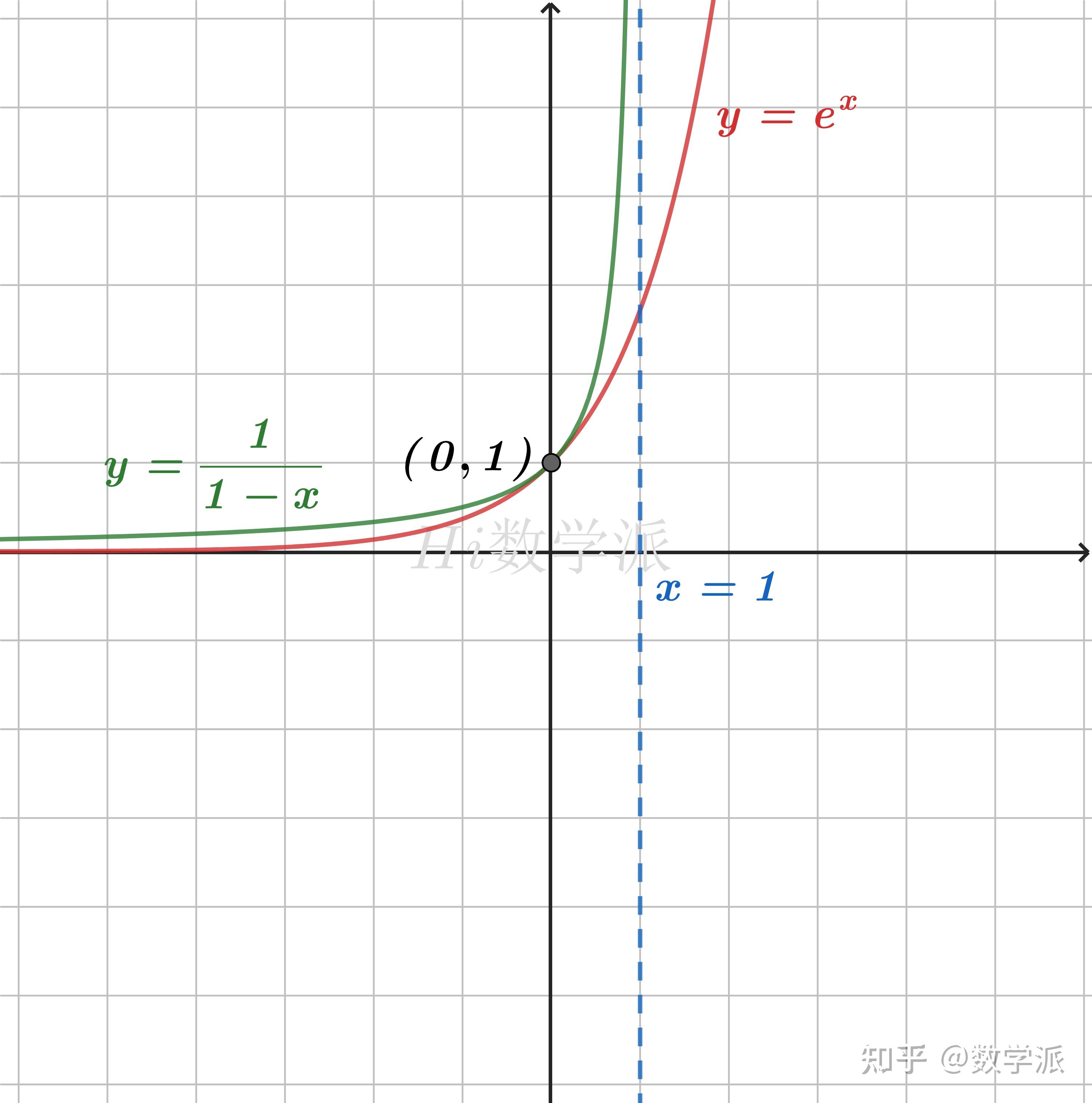
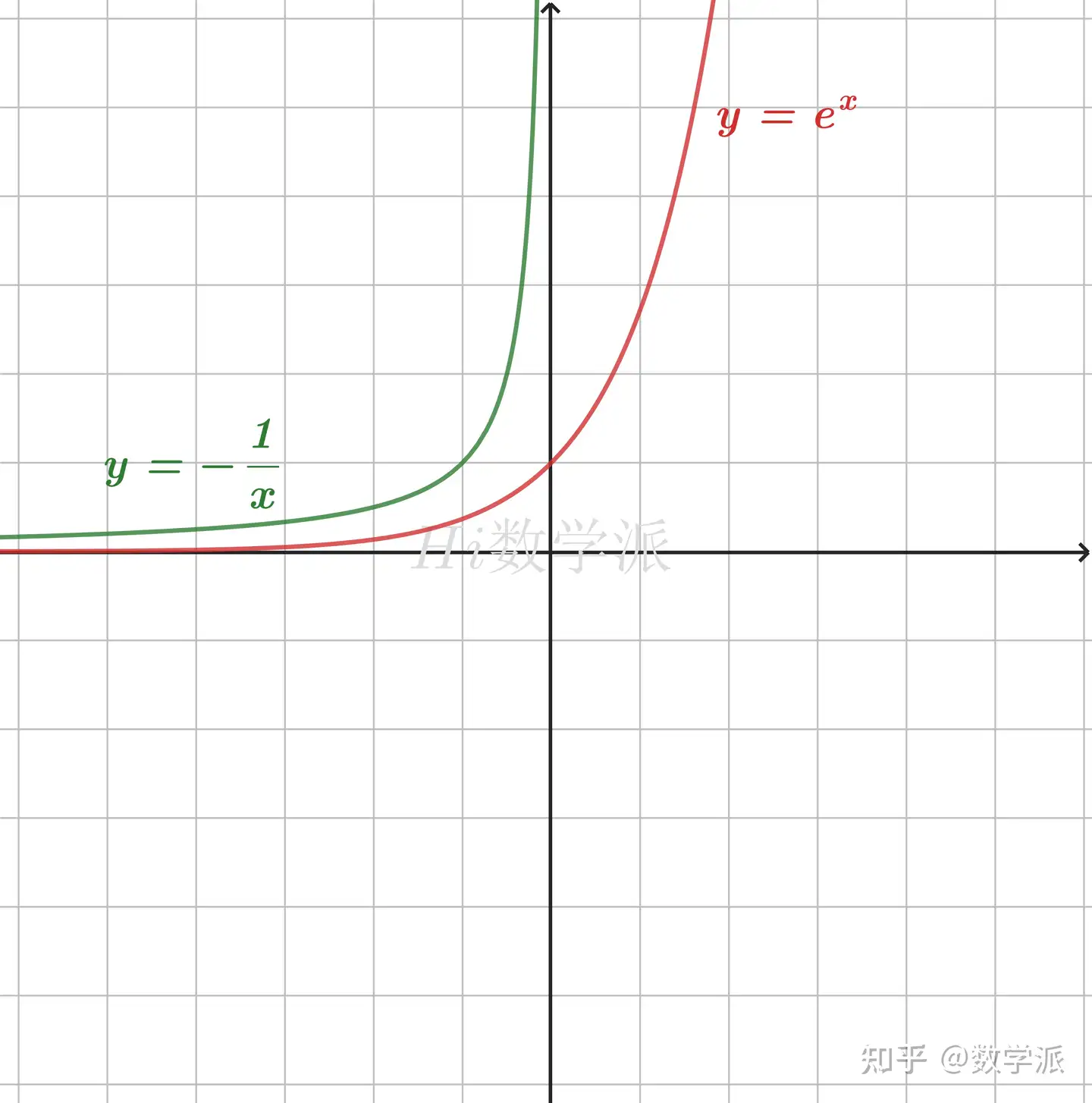
- ex<−x1,(x<0)
放缩成高幂次函数
- ex≥1+x+21x2,(x≥0) (仅当x=0时取等号)
- ex≤1+x+21x2,(x≤0) (仅当x=0时取等号)
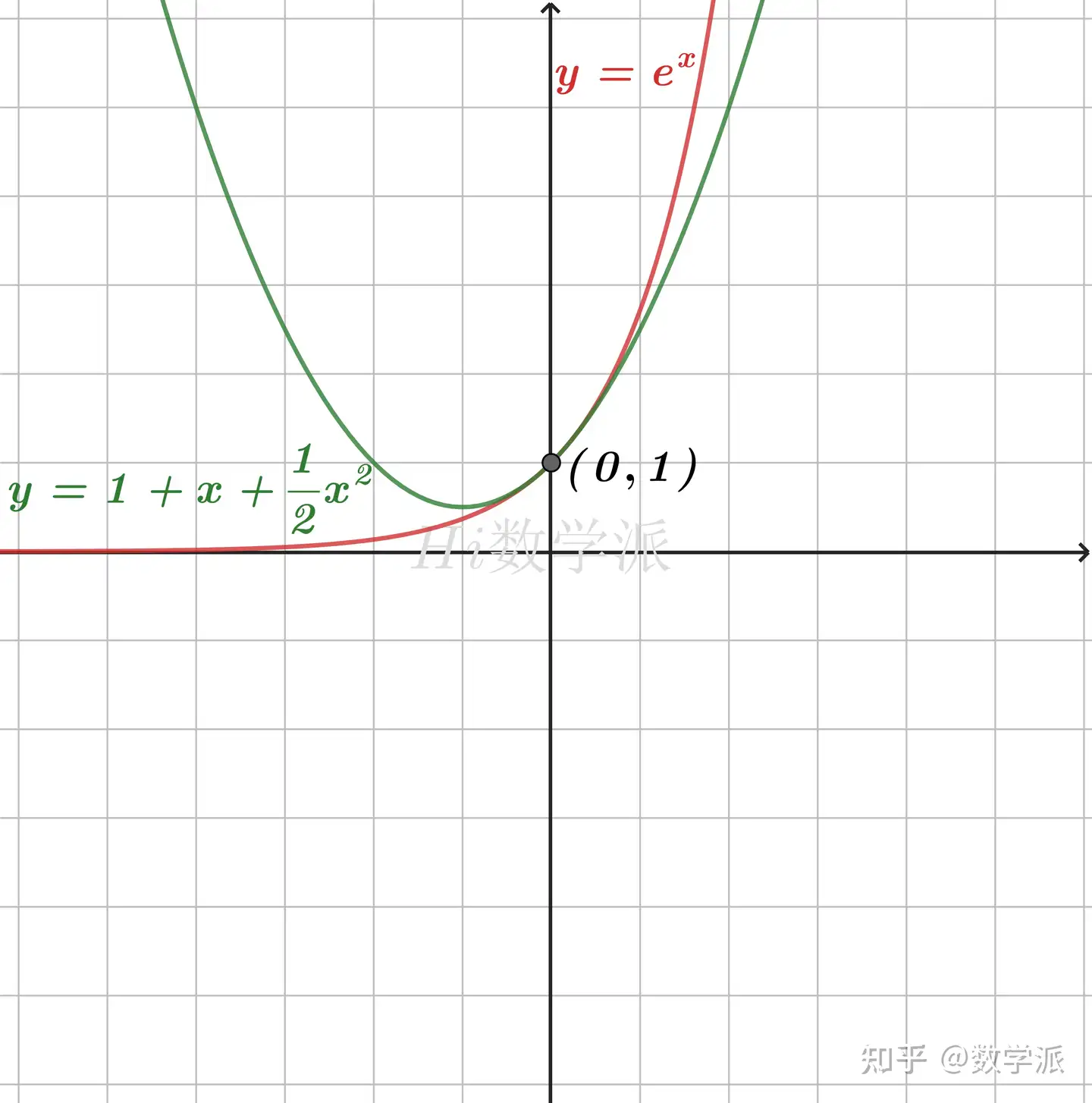
- ex≤1+x+21x2+61x3 (仅当x=0时取等号)
对数函数放缩
放缩成一次函数
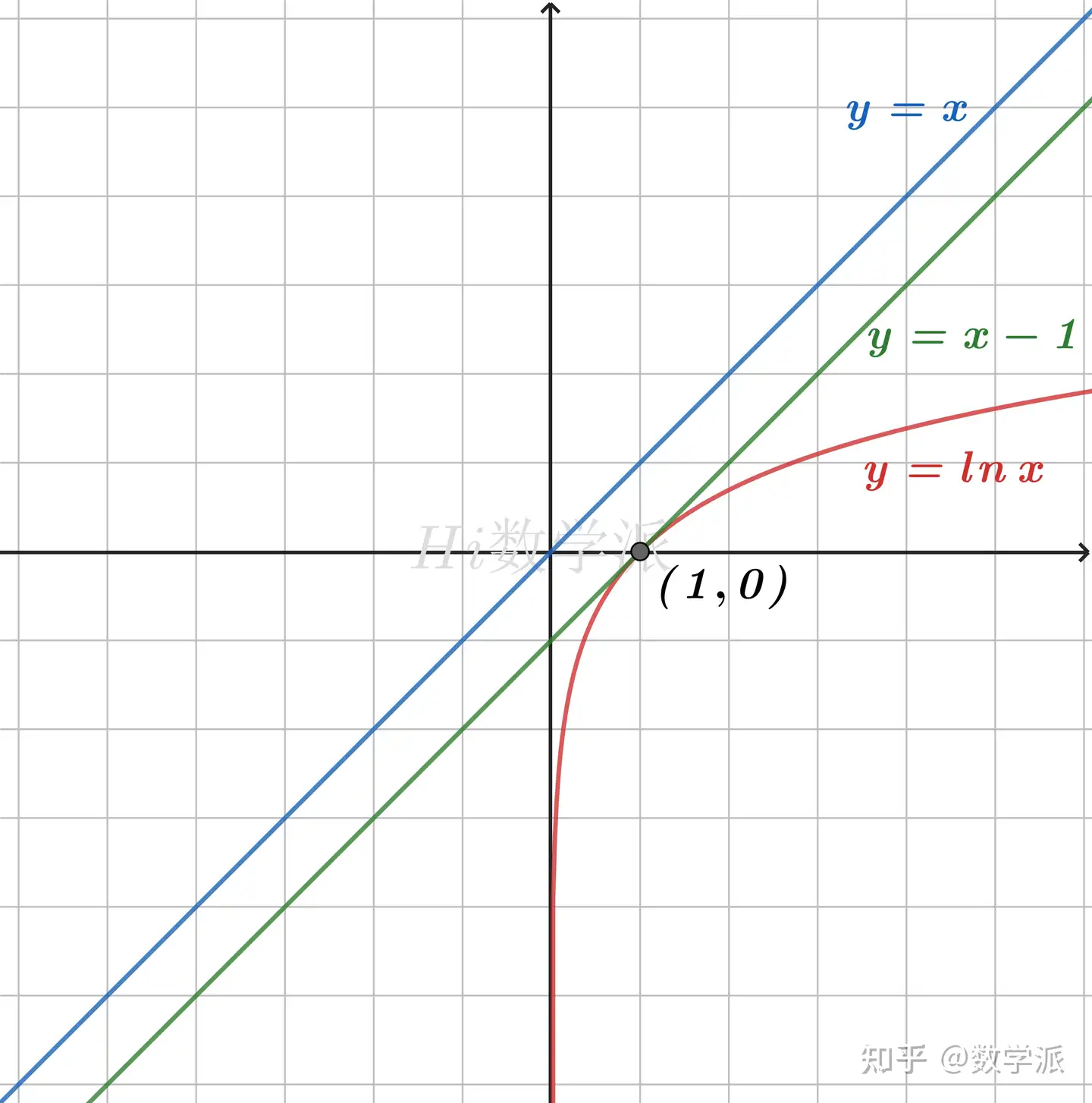
- ln(x+1)≤x (仅当x=0取等号)

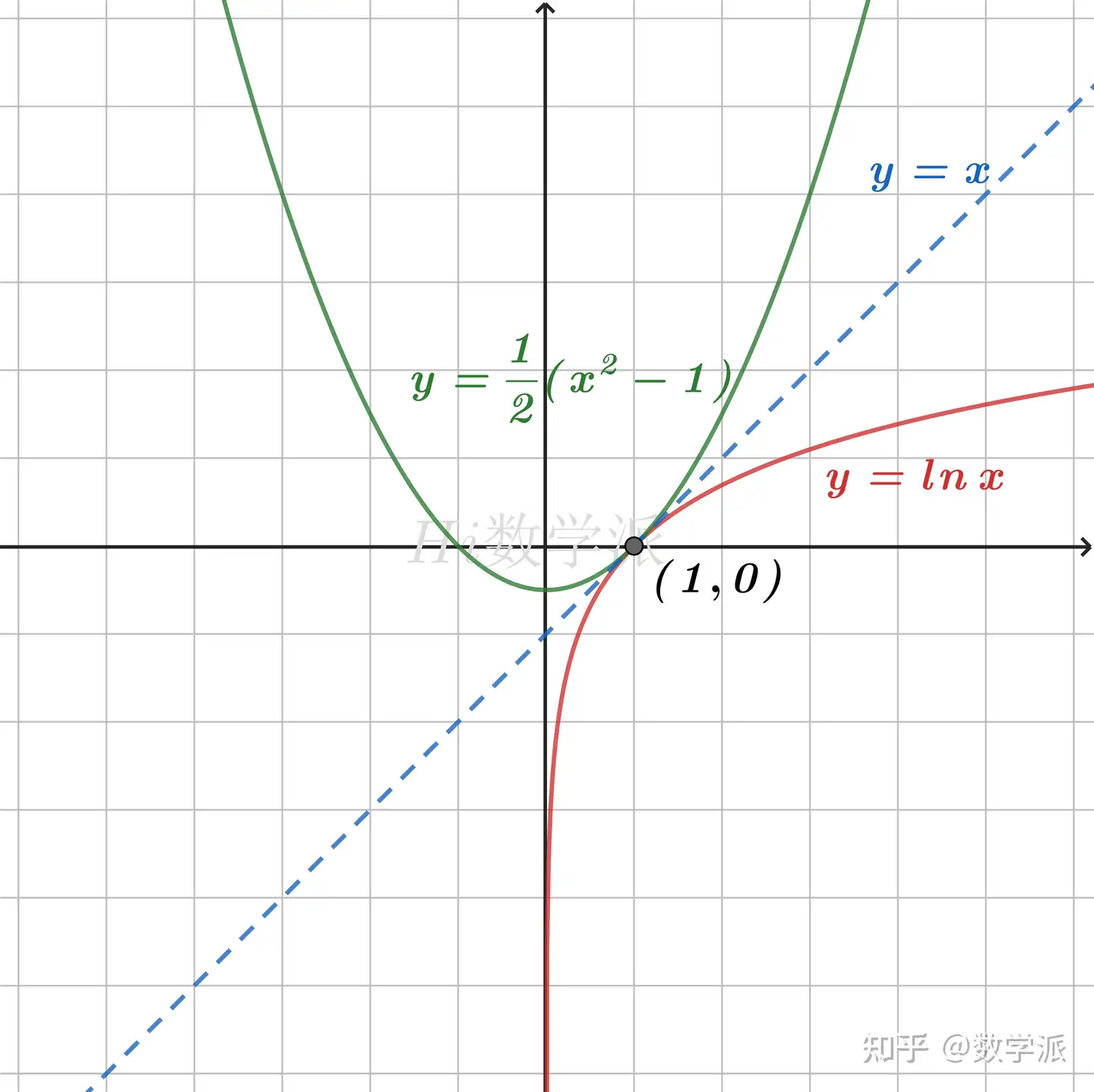
- lnx≤x−1<x (仅当x=1时取等号)
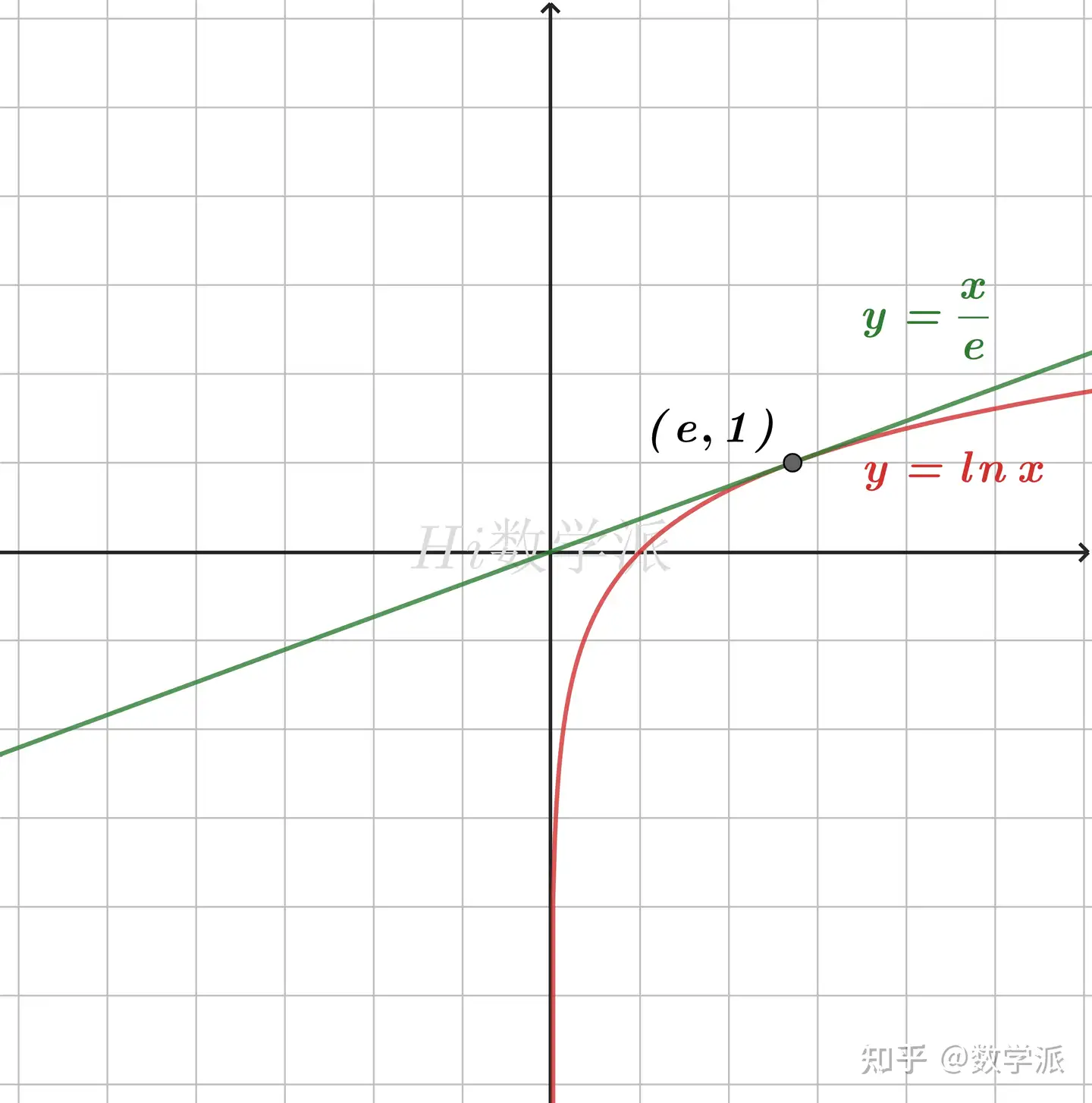
- lnx≤ex (仅当x=e时取等号)
放缩成双撇函数
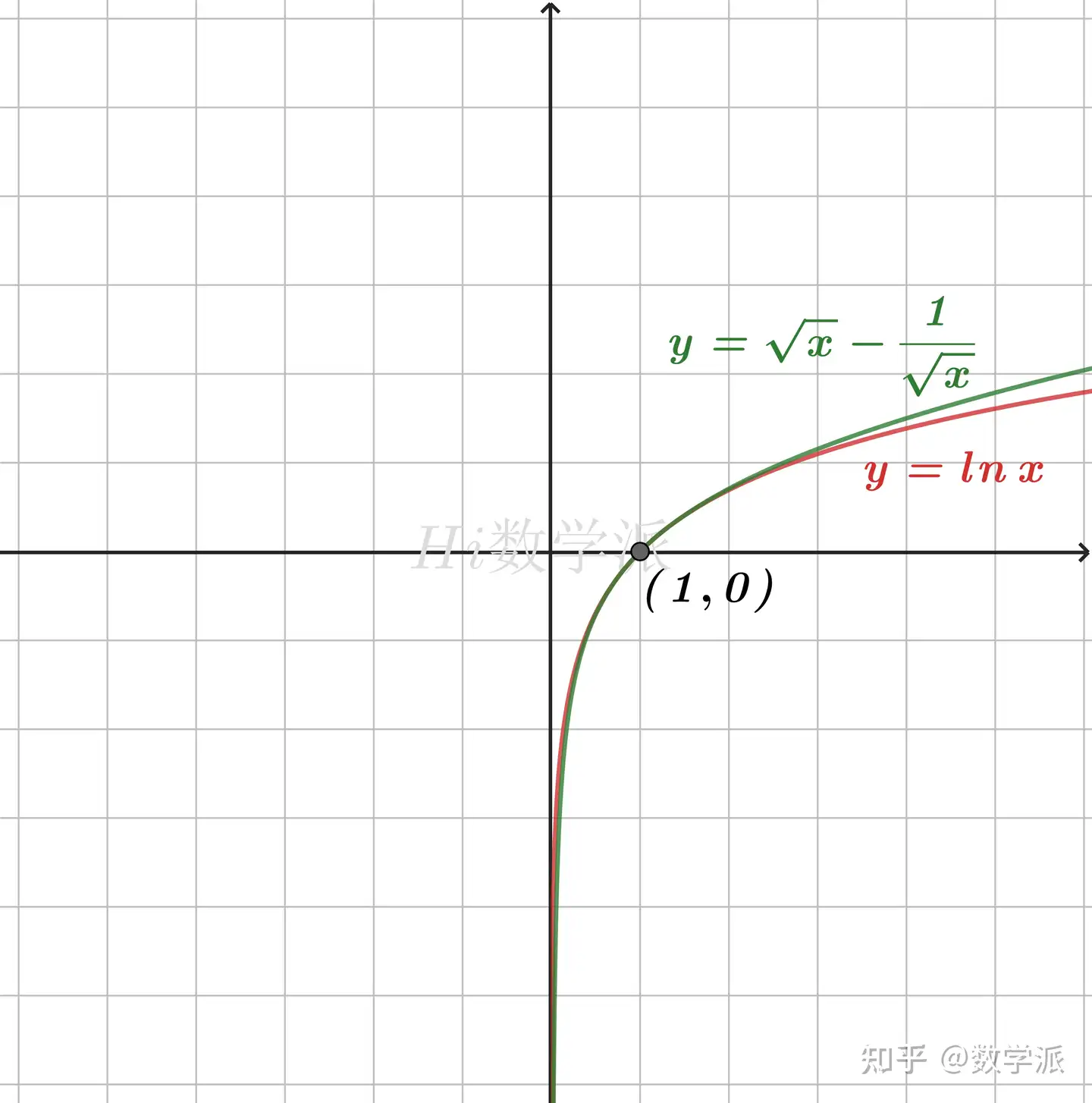
- lnx≥21(x−x1),(0<x≤1) (仅当x=1时取等号)
- lnx≤21(x−x1),(x≥1) (仅当x=1时取等号)

- lnx≥x−x1,(0<x≤1) (仅当x=1时取等号)
- lnx≤x−(1x),(x≤1) (仅当x=1时取等号)
放缩成类反比例函数
- lnx≥1−x1 (仅当x=1时取等号)
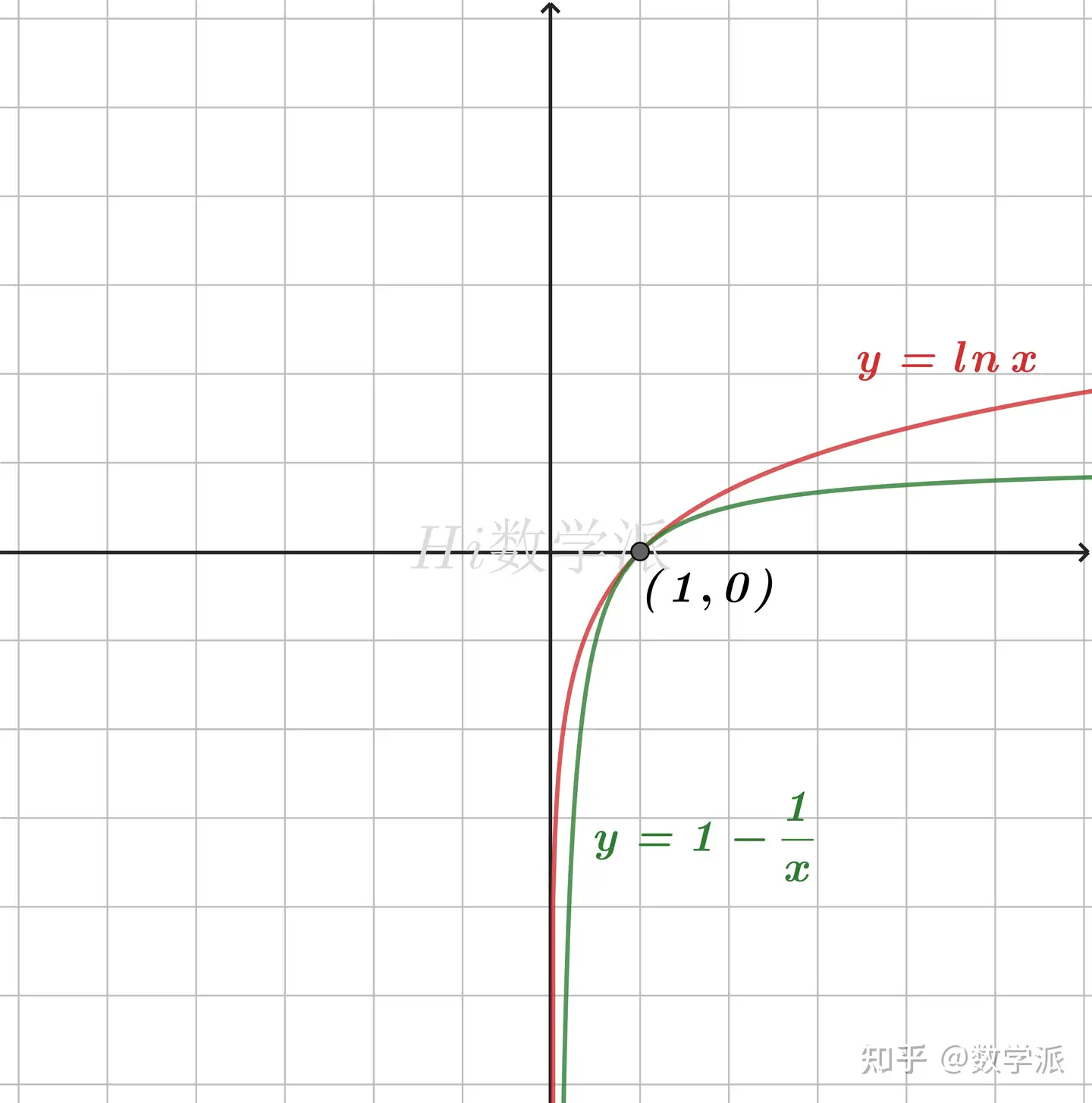
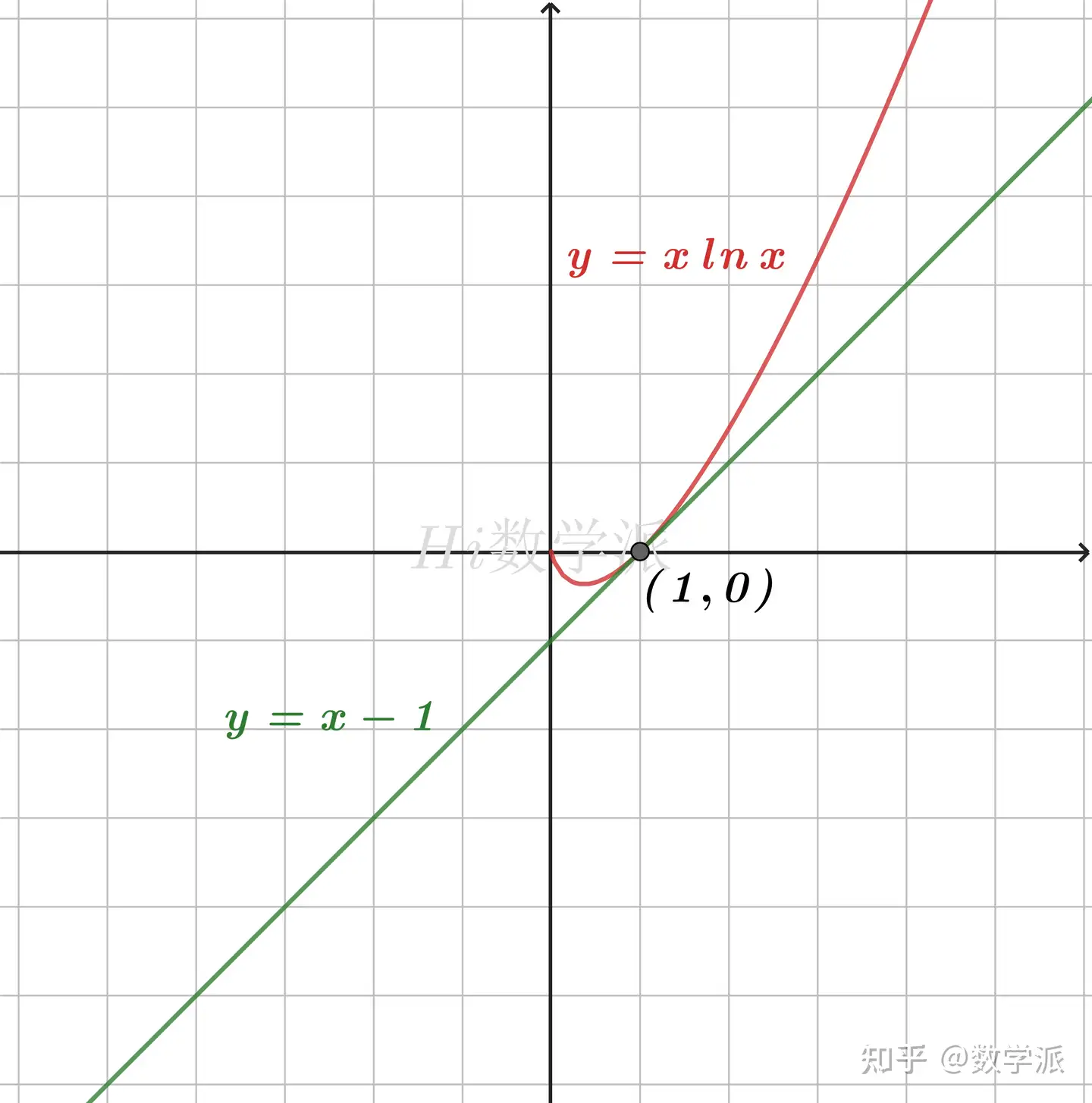
- xlnx≥x−1 (仅当x=1时取等号)
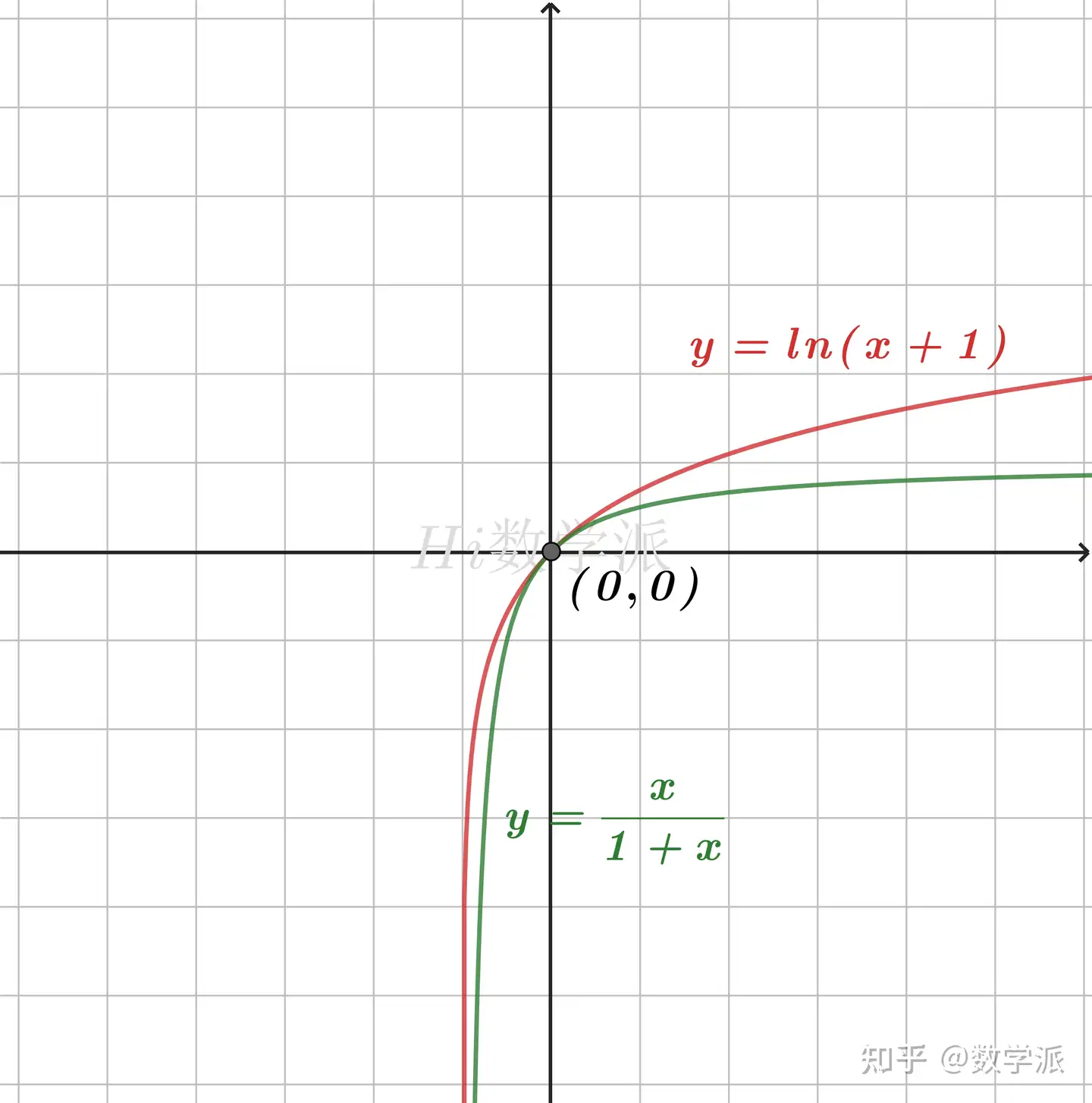
- ln(x+1)≥1+xx (仅当x=0时取等号) `(遇到过)`
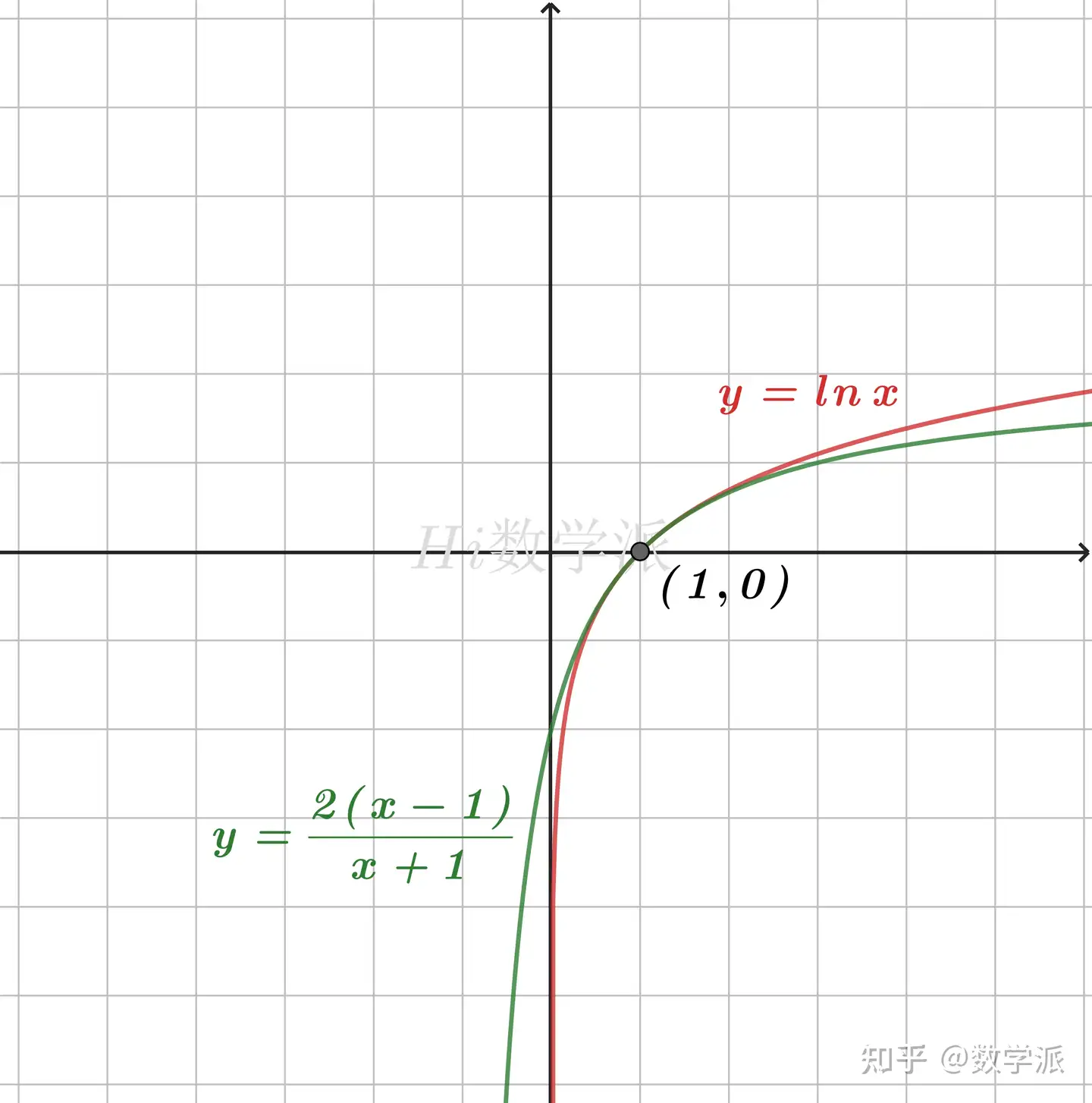
- lnx≤x+12(x−1),(0<x≤1) (仅当x=1时取等号)
- lnx≥x+12(x−1),(x≥1) (仅当x=1时取等号)
- ln(x+1)≤x+22x,(−1<x≤0) (仅当x=0时取等号)
- ln(x+1)≥x+22x,(x≥0) (仅当x=0时取等号)
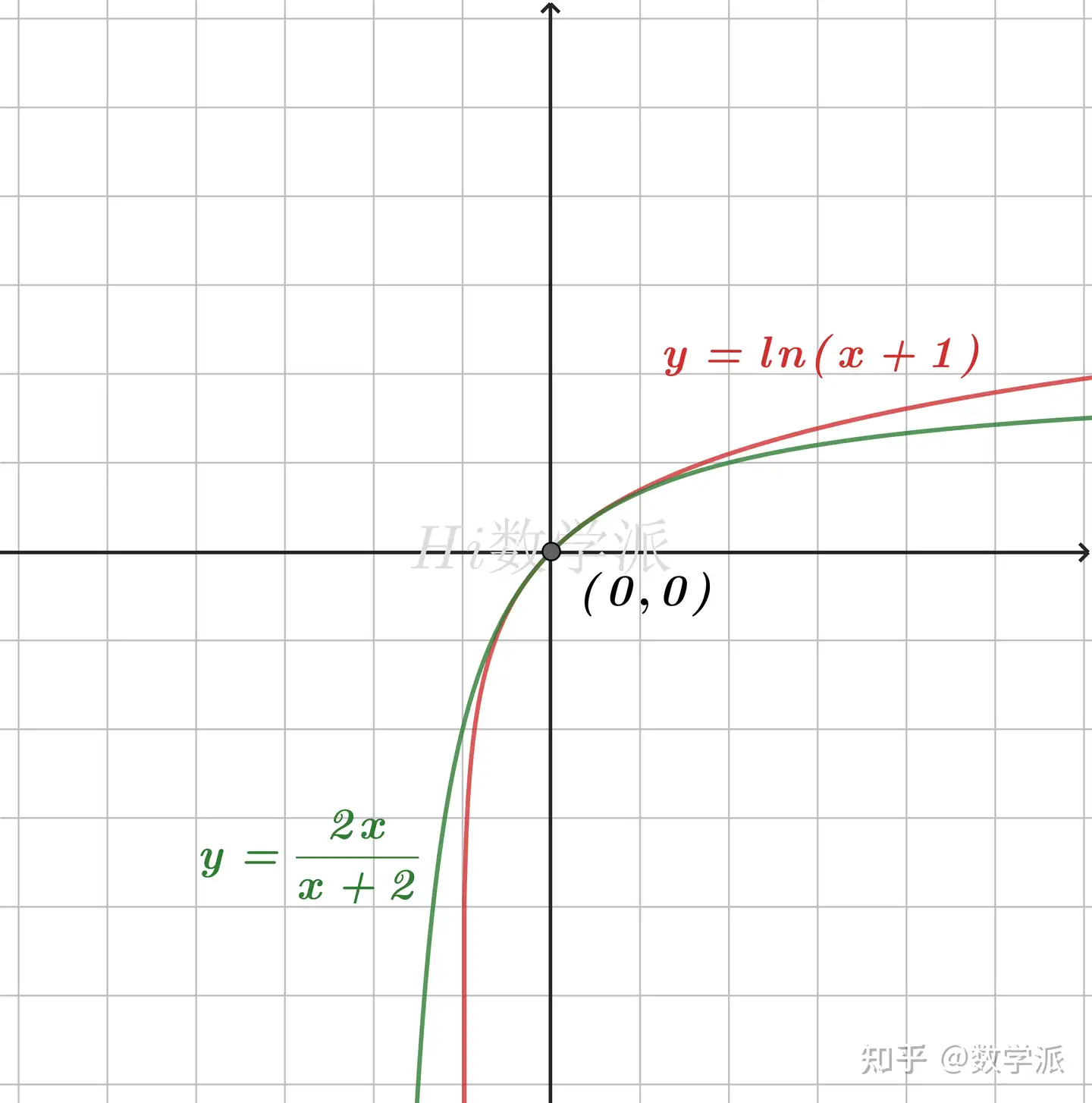
放缩成二次函数
- lnx≤x2−x (仅当x=1时取等号)

- lnx≤21(x2−1) (仅当x=1时取等号)
- ln(1+x)≤x−21x2,(−1<x≤0) (仅当x=0时取等号)
- ln(1+x)≥x−21x2,(x≥0) (仅当x=0时取等号)

指对混合放缩
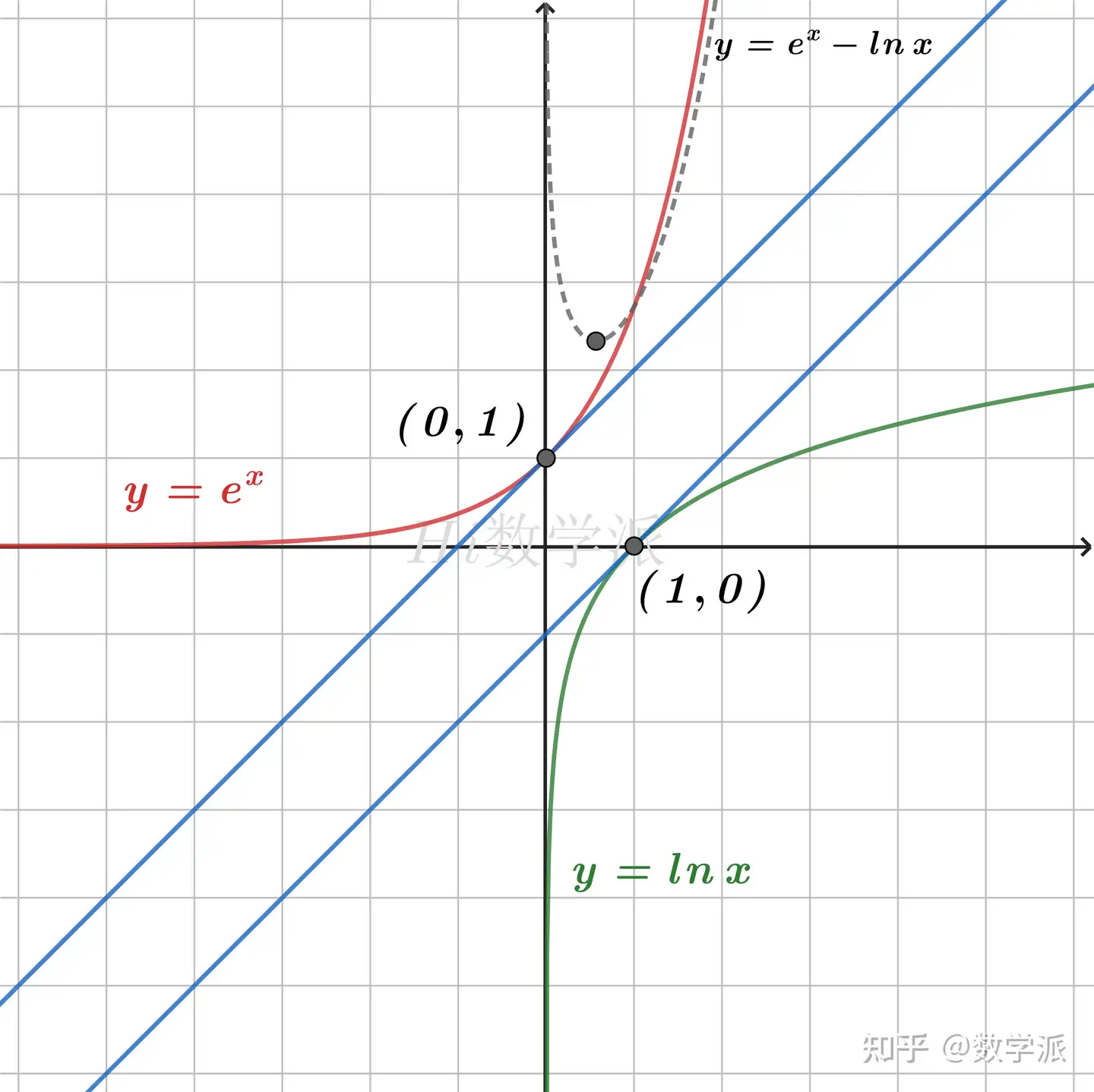
- ex−lnx>(x+1) (仅当x=时取等号)
证明: 将不等式 ex≥x+1 (仅当x=0时取等号)和 lnx≤x−1 (仅当x=1时取等号)相减即可得。因为两不等式等号不能同时取到,故该不等式为严格不等号。
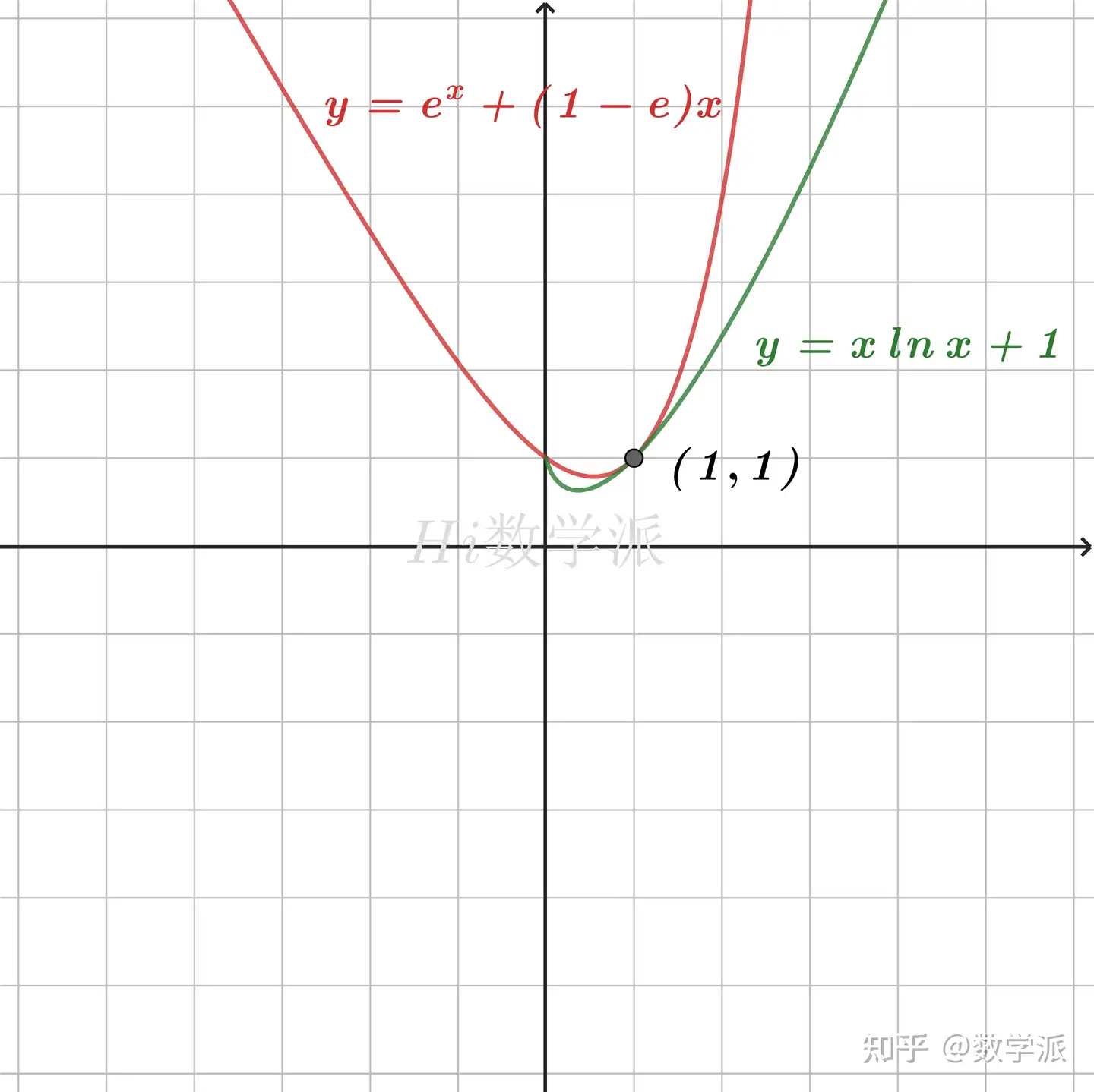
- ex+(1−e)x≥xlnx+1 (仅当x=1时取等号)

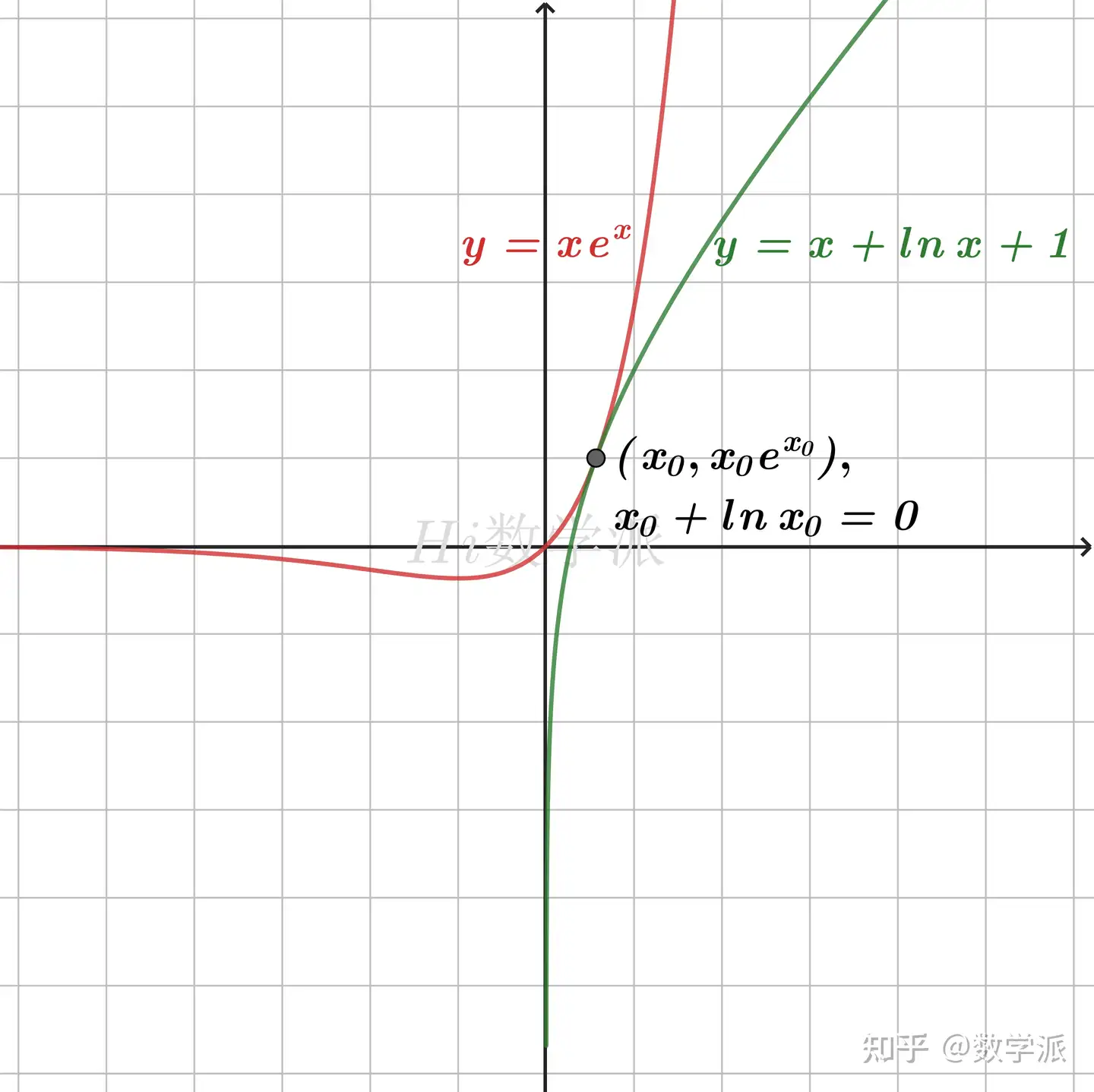
- xex≥x+lnx+1 (仅当x+lnx=0时取等号) (朗博不等式)
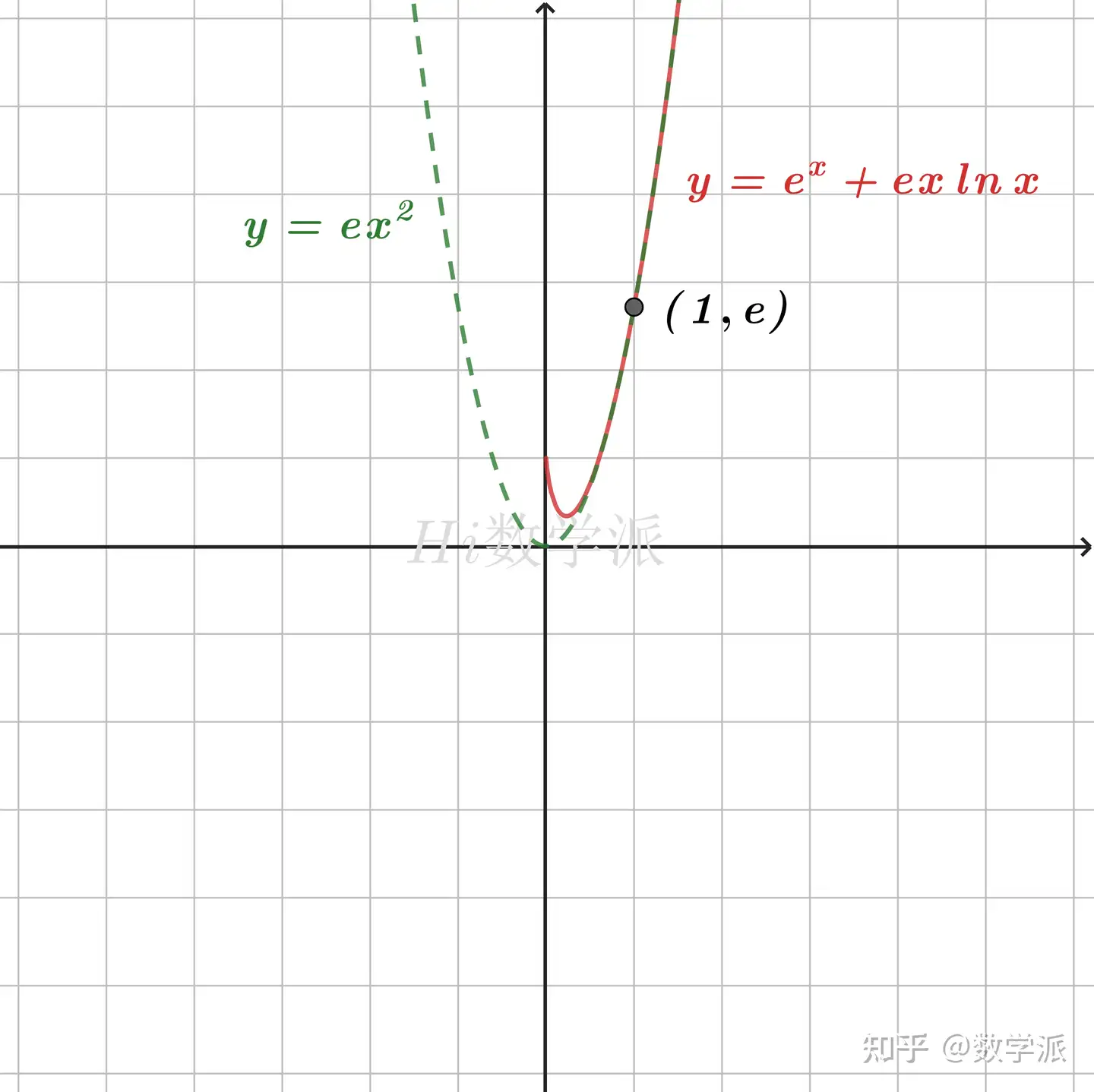
- ex+exlnx≥ex2 (仅当x=1时取等号)
三角函数放缩
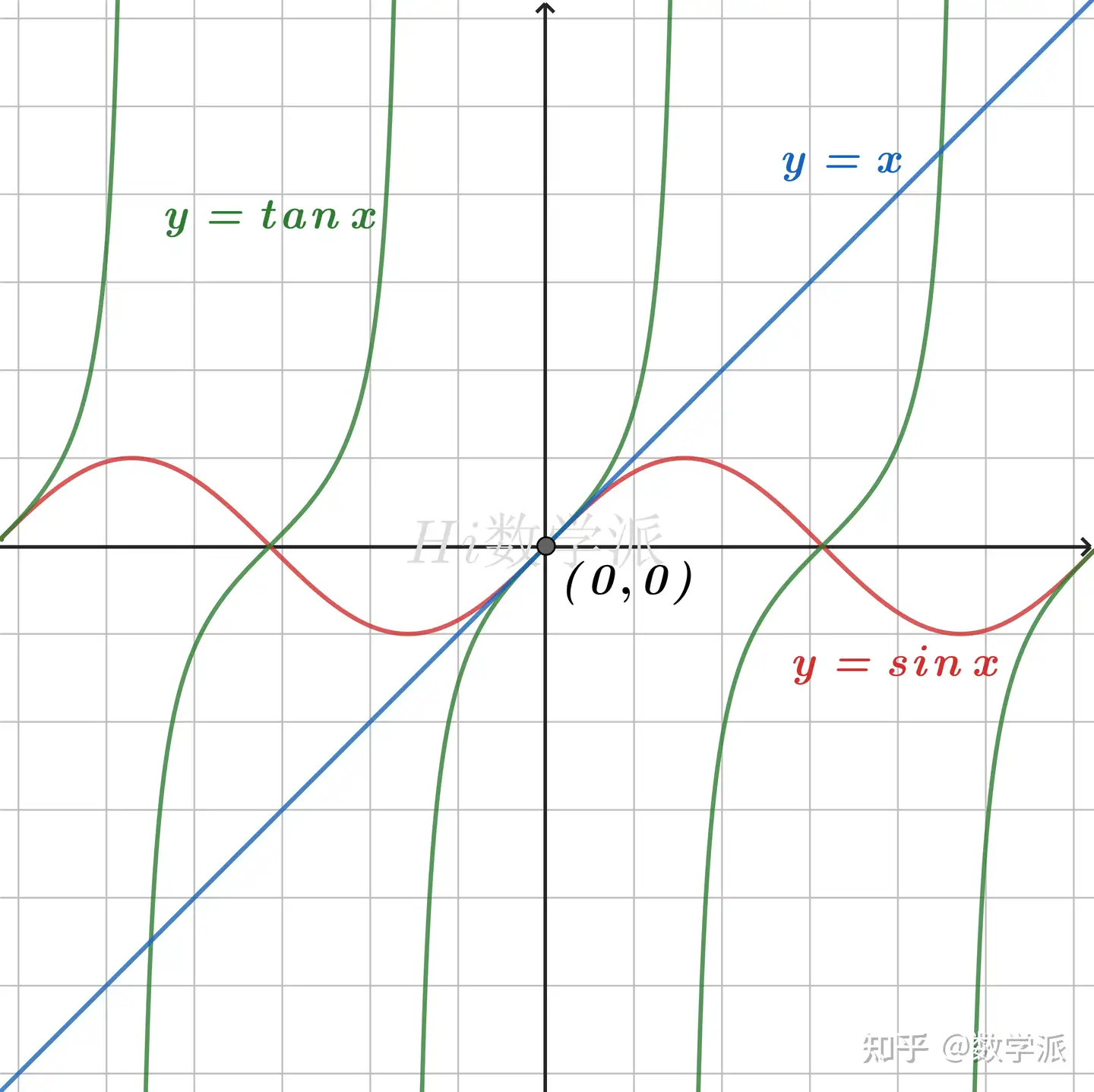
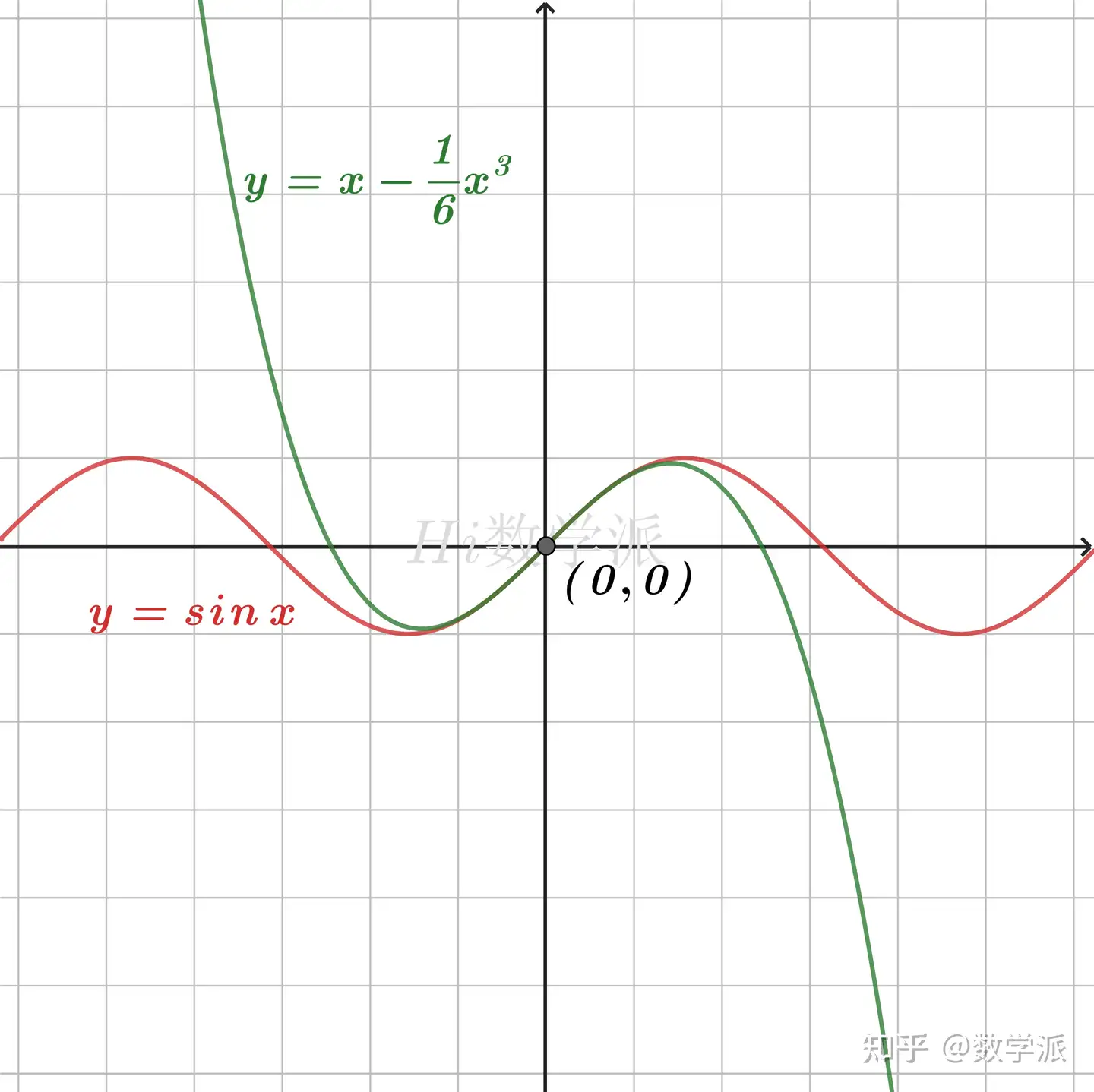
- sinx≤x≤tanx,(0≤x<2π) (仅当x=0时取等号) `数学归纳题常用`
- sinx≥x≥tanx,(−2π<x≤0) (仅当x=0时取等号) `数学归纳题常用`
- arctanx≤x≤arcsinx(0≤x≤1)
- sinx<x(x>0)
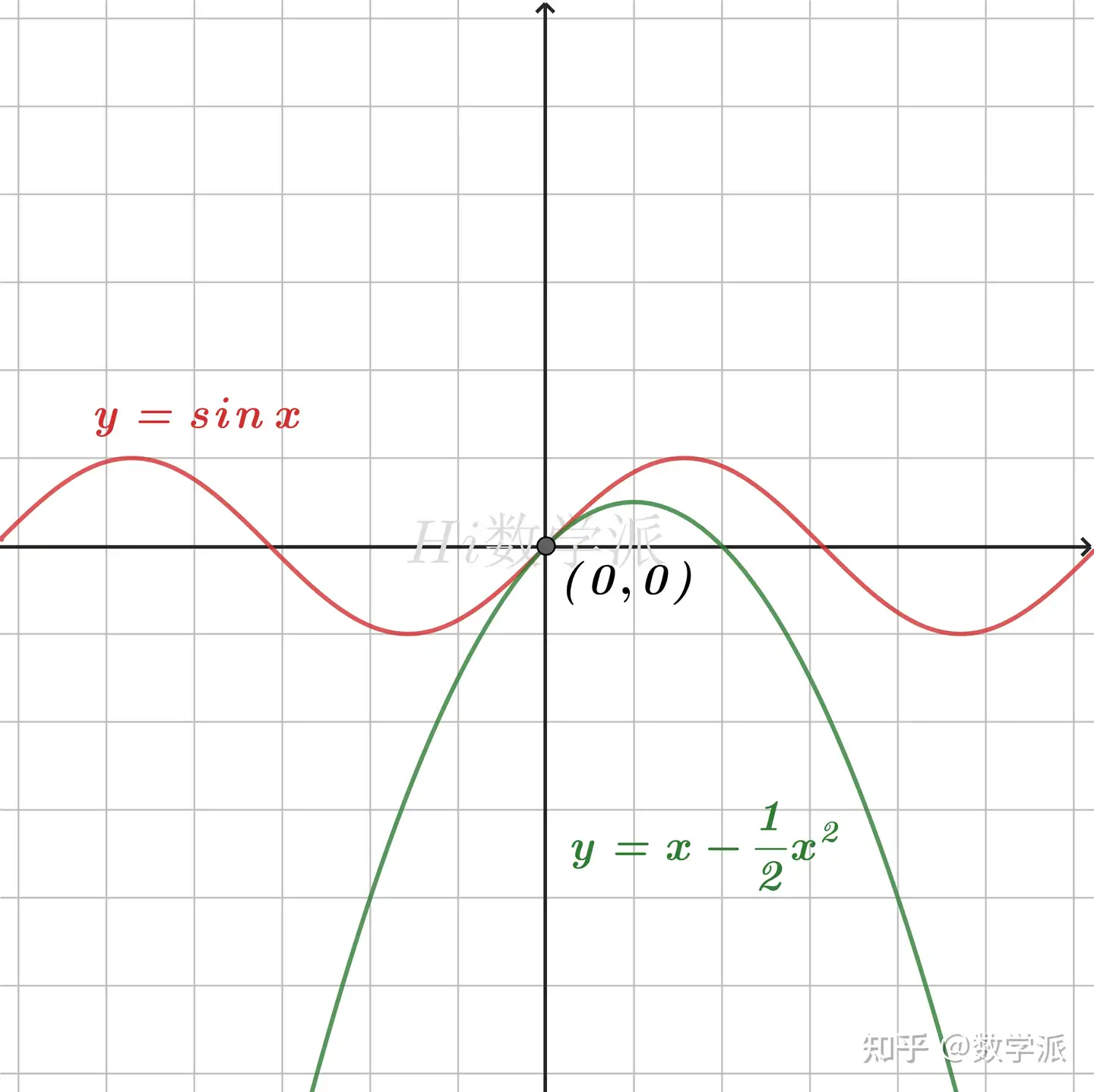
- sin≥x−21x2 (仅当x=0时取等号)
- cosx≥1−21x2 (仅当x=0时取等号)

- sinx≤x−61x3,(x≤0) (仅当x=0时取等号)
- sinx≥x−61x3,(x≥0) (仅当x=0时取等号)
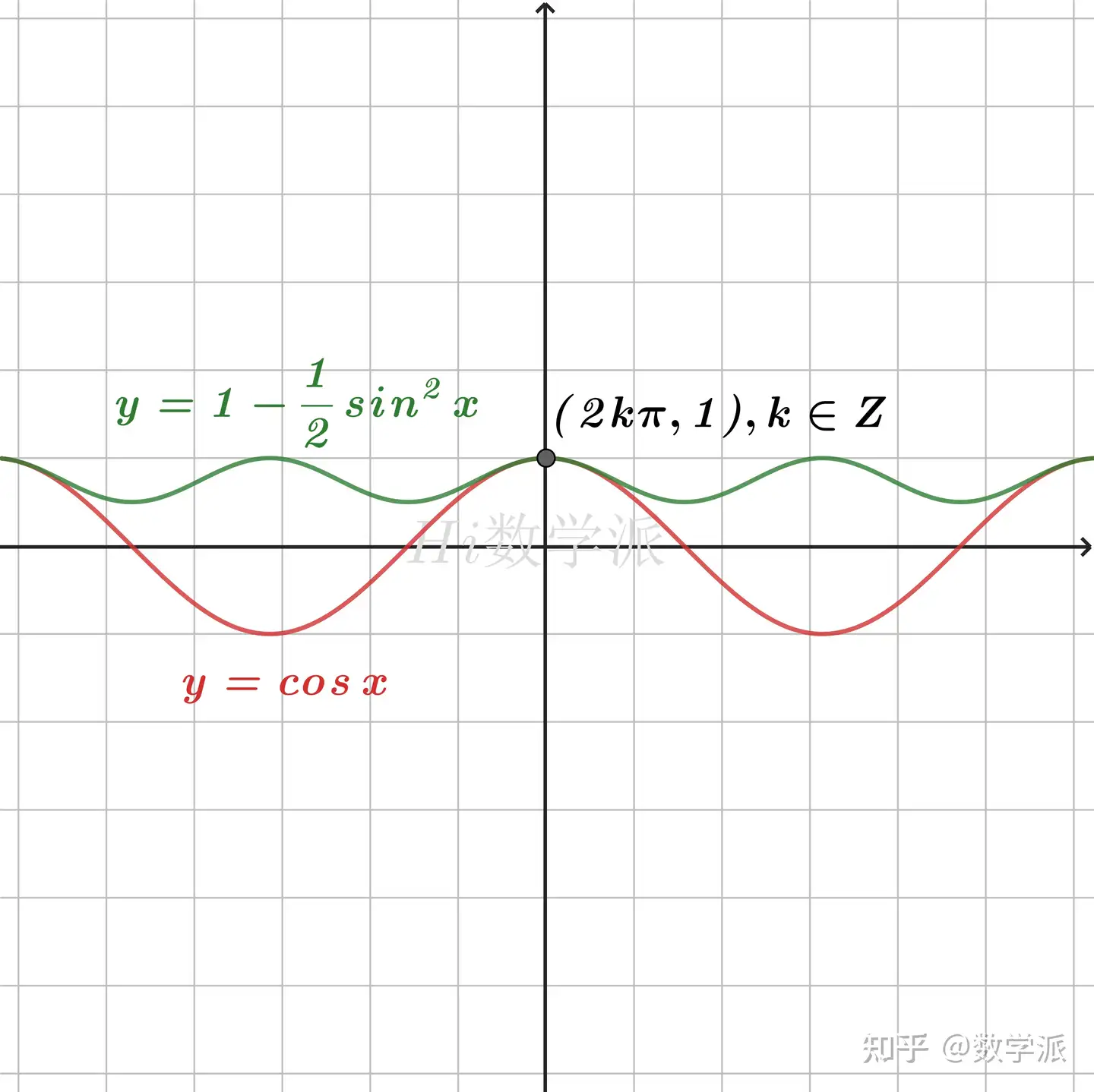
- cosx≤1−21sin2x (仅当 x=2kπ,k∈Z 时取等号)
笔记
函数极限
反函数
- x=f−1(y)的图像与y=f(x)完全重合;y=f−1(x)的图像和y=f(x)关于y=x对称。
- 有反函数的函数不一定是单调函数。(p4)
有界性
- 不知区间,无法谈论有界性。证明有界性需要用y=-M和y=M包住。
奇偶性
- -f(-x)与f(x)图像关于
原点对称。
- f(x)+f(-x)必是偶函数;f(x)-f(-x)必是奇函数。任何一个函数都可以写成
奇函数+偶函数的形式。
- 求导奇偶性会换;积分f(x)⇒∫0xf(t)dt奇偶性会换。
设对任意的x,y,都有f(x+y)=f(x)+f(y),则f(x)是奇函数。
证明:令x=y=0,则f(0)=f(0)+f(0),f(0)=0;再令y=-x,则f(0)=f(x)+f(-x),即f(-x)=f(x),故f(x)是奇函数。
周期性
- 若f(x)以T为周期,则f(ax+b)以∣a∣T为周期。
- 若g(x)是周期函数,则复合函数f[g(x)]也是周期函数,如 esinx,cos2x 等。
- 若f(x)是以T为周期的可导函数,则f′(x)也以T为周期。
- 若f(x)是以T为周期的连续函数,则只有在∫0Tf(x)dx=0时,∫0xf(t)dt也以T为周期。
最值
- 看到u1,可用u来研究最值。(结论相反,即两者的最大值点、最小值点相反)。
指数函数
- (aα)β=aαβ(a是正实数,α,β是任意实数)
有界性
- 若y=f(x)在[a,b]上为连续函数,则f(x)在[a,b]上必定有界。
- 若f(x)在(a,b)内为连续函数,且x→a+limf(x)与x→b−limf(x)都存在,则f(x)在(a,b)内必定有界。
- 有界函数与有界函数的和、差、积仍为有界函数。
极限的局部保号性
- limf>0⇒f>0
- f≤0∣∣f<0⇒limf≤0
(只讨论0?)
不同函数在x->∞时比大小
- 当 x → +∞ 时,有lnαx≪xβ≪ax,其中α,β>0,a>1,符号“≪”叫远远小于。
- 当 n → ∞ 时,有lnαn≪nβ≪an≪n!≪nn,α,β>0,a>1 .
数列极限
子列
等差数列
- 首项为a1,公差为d(d≠0)的数列
- a1,a1+d,a1+2d,⋯,a1+(n−1)d,⋯.
- 前n项的和Sn=2n[2a1+(n−1)d]=2n(a1+an).
等比数列
- 首项为a1,公比为r(r≠0)的数列
- a1,a1r,a1r2,⋯,a1rn−1,⋯.
- 前n项的和Sn={na1,1−ra1(1−rn),r=1,r=1.
常见数列求和公式
- k=1∑nk2=12+22+32+⋯+n2=6n(n+1)(2n+1). [推导过程](https://www.hanspub.org/journal/PaperInformation?paperID=65537)
- k=1∑nk3=13+23+33+⋯+n3=(2n(n+1))2. (书中没写)
- k=1∑nk(k+1)1=1×21+2×31+3×41+⋯+n×(n+1)1=n+1n.
推导:(裂项)=1−21+21−31+31−41+⋯+n1−n+11
一个重要数列的结论
- 数列(1+n1)n单调递增
- n→+∞lim(1+n1)n=e.
绝对值-极限问题
- 结论:若n→∞liman=A,则n→∞lim∣an∣=∣A∣.
证明:∵n→∞liman=A,∴对任意正数ε,存在正整数N,当n>N时,有∣an−A∣<ε.
又由不等式∣∣a∣−∣b∣∣≤∣a−b∣,有∣∣an∣−∣A∣∣≤∣an−A∣<ε. 故n→∞lim∣an∣=∣A∣.
- 此命题反过来不对,如取an=(−1)n,则n→∞lim∣(−1)n∣=1.但n→∞lim(−1)n不存在。
- 在本题中若A=0,则∣∣an∣−∣A∣∣=∣∣an∣−0∣=∣an−0∣,即有n→∞liman=0⇔n→∞lim∣an∣=0,这个结论常用。
- ∴n→∞lim∣xn−a∣=0⇒n→∞limxn−a=0→n→∞limxn=a
- 一般地,若要证n→∞liman=0,可转化为证n→∞lim∣an∣=0,由于∣an∣≥0,若使用夹逼准则,则省了一半的力气,只需找到一个数列 bn 满足∣an∣≥bn,且n→∞limbn=0即可。
- 此结论对函数亦成立,即若x→x0limf(x)=A,则x→x0lim∣f(x)∣=∣A∣.
收敛数列的性质-唯一性
海涅定理(归结原则)
- 设 f(x) 在 U˚(x0,δ) 内有定义,则 x→x0limf(x)=A存在⇔对任何 U˚(x0,δ) 内以 x0 为极限的数列 xn(xn=x0) ,极限n→∞limf(x0)=A存在。
放缩的常用方法
- n⋅umin≤u1+u2+⋯+un≤n⋅umax.
- 当ui≤0时,1⋅umax≤u1+u2+⋯+un≤n⋅umax.
- 设a,b为实数,则
- ∣a±b∣≤∣a∣+∣b∣
- ∣∣a∣−∣b∣∣≤∣a−b∣
- 推广:(n个实数)∣a1±a2±⋯±an∣≤∣a1∣+∣a2∣+⋯+∣an∣.
- (a,b≤0)ab≤2a+b≤2a2+b2
- ∣ab∣≤2a2+b2
例如:若un>0,则nun=un⋅n1≤2un2+n21.
- (a,b,c≥0)3abc≤3a+b+c≤33a2+b2+c2
- 设a≥b≥0,则{m>0,m<0,am≥bmam≤bm
- 若 0 < a < x < b , 0 < c < y < d ,则bc<xy<ad.
- 考研中考过:当nπ<x<(n+1)π,2n<S(x)<2(n+1)时,(n+1)π2n<xS(x)<nπ2(n+1).
- sinx<x<tanx(0<x<2π).
- sinx<x(x>0).
- 考研中考过:当xn>0时,xn+1=sinxn<xn,故xn单调减少.
- 当0<x<4π时,x<tanx<π4x
- 当0<x<2π时,sinx>π2x
- arctanx≤x≤arcsinx(0≤x≤1)
- 可考:当xn>0时,xn+1=arctanxn<xn,故xn单调减少.
- ex≥x+1(∀x)
- 可考:当xn+1=exn−1时,由exn−1≥xn,得xn+1≥xn,即xn单调不减.
- x−1≥lnx(x>0)
- 可考:当xn>0时,若xn+1=lnxn+1,由lnxn+1≤xn,得xn+1≤xn,即xn单调不增.
- 1+x1<ln(1+x1)<x1(x>0)或1+xx<ln(1+x)<x(x>0).
- 利用闭区间上连续函数必有最大值与最小值.
- 利用压缩映射原理.
- 原理一 对数列xn,若存在常数 k (0 < k < 1),使得∣xn+1−a∣≤k∣xn−a∣,n=1,2,⋯,则xn收敛于a.
- 证明 0≤∣xn+1−a∣≤k∣xn−a∣≤k2∣xn−1−a∣≤⋯≤kn∣x1−a∣,由于n→∞limkn=0,根据夹逼准则,有n→∞lim∣xn+1−a∣=0,即xn收敛于a.
- 原理二 对数列xn,若xn+1=f(xn),n=1,2,⋯,f(x)可导,a是f(x)=x的唯一解,且∀x∈R,有∣f′(x)≤k<1,则xn收敛于a.
- 证明 ∣xn+1−a∣=∣f(xn)−f(a)∣拉格朗日中值定理∣f′(ξ)∣∣xn−a∣≤k∣xn−a∣,其中ξ介于a与xn之间,由原理一,有xn收敛于a.
- 以上原理一、二是特殊的压缩映射过程,考生在使用它们时,要写出证明过程。
- 利用题设条件来推证。(这往往是大题的第1问)
单调有界准则
- 单调有界数列必有极限,即若数列xn单调增加(减少)且有上界(下界),则n→∞limxn存在.
- 证明数列xn单调性的常用方法:
- xn+1−xn>0(<0)或xnxn+1>1(<1)
- 利用数学归纳法
- 利用重要不等式(a2+b2)≥2ab之类)
- xn−xn−1与xn−1−xn−2同号,则数列xn单调.
- 利用结论:对xn+1=f(xn)(n=1,2,⋯),xn∈区间 I.
- 若f’(x)>0,x∈区间 I,则数列xn单调,且{当x2>x1时,数列xn单调增加当x2<x1时,数列xn单调减少
- 若f’(x)<0,x∈区间 I,则数列xn不单调.
含绝对值函数的可导性讨论
含绝对值函数的可导性讨论